Assignment #4
Nicole Mosteller
EMAT 6680

Assignment #4: Investigation #8. 
Begin with acute DABC. Construct DMIG and DFDE (see instructions below).
Prove DMIG is congruent to DFDE.

Figure 1.

To construct DMIG(see Figure 2): Let pt. M be the midpoint of segment BC, pt. I be the midpoint of segment AB, and pt. G be the midpoint of segment AC. By definition, DMIG is a medial triangle.


Figure 2.
How do the sides of DMIG relate to the sides of DABC?

Because the vertices of DMIG are all midpoints of DABC, DMIG is a medial triangle whose sides are midsegments of DABC. Since the sides are midsegments, we can conclude:



. 
Click here! to see why the midsegment is half the length of its corresponding side.

To construct DFDE(see Figure 3): Construct the orthocenter (pt. H) of DABC. Click here! to see that DFDE can be constructed with pt. H anywhere inside the original triangle (not just at the orthocenter). To construct DFDE, first connect the vertices of DABC and the pt. H creating segments CH, BH, and AH. Let pt. D be the midpoint of segment CH, pt. E be the midpoint of segment BH, and pt. F be the midpoint of segment AH. When using the orthocenter, pt. H, as a vertex, DFDE is called a midsegment triangle.

Figure 3.

How do the sides of DFDE relate to the sides of DABC?

To see this relation, it is necessary to use the smaller triangles that have the common vertex H 
(DBCH, DABH, and DCAH. In DBCH, notice that pts. E and D are midpoints of two of its sides.
This means that segment ED is a midsegment of DBCH, and
.
In DABH, pts. F and E are midpoints of two of its sides.
By definition, segment EF is a midsegment of DABH, and 
.
In DCAH, pts. F and D are midpoints of two of its sides.
By definition, segment FD is a midsegment of DCAH, and 
.

Let's compile the conclusions made on Figure 2 and Figure 3.
               
                
               
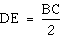
Using the transitive property, we can now conclude :
MI = FD
IG = DE
GM = EF.
By SSS, DMIG is congruent to DFDE.


Return to Nicole's Page