
Final Project Nicole Mosteller EMAT 6680
Given point P inside DABC with segments AD, BE, and CF containing point P. Investigate the relationship between (AF)(BD)(CE) and (FB)(DC)(EA).
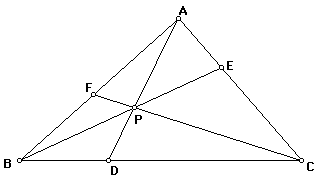
From the investigation of DABC, the following data was collected:
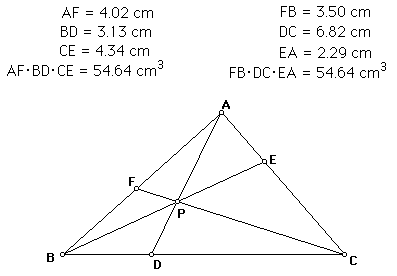 Similar data was collected for various locations of point P.
This investigation has led me to the following conjecture:
Given point P inside DABC with segments AD, BE, and CF containing point P,
then the ratio (AF)(BD)(CE):(FB)(DC)(EA) is 1.
Similar data was collected for various locations of point P.
This investigation has led me to the following conjecture:
Given point P inside DABC with segments AD, BE, and CF containing point P,
then the ratio (AF)(BD)(CE):(FB)(DC)(EA) is 1.
To begin this proof, it is necessary to add a few auxillary lines to DABC. The auxillary lines that have been added are parallel to BE - one through point A and the other through point C (see Figure 1).
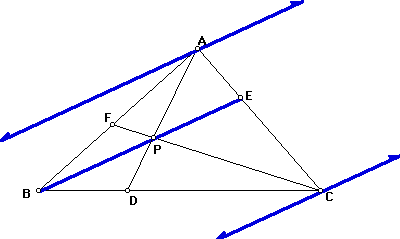 Figure 1: Additional parallel lines through A and C.
Figure 1: Additional parallel lines through A and C.
In addition to the parallel lines, I have altered the original DABC by extending CP to intersect the new line through A at point J and by extending AP to intersect the new line through C at point K (see Figure 2).
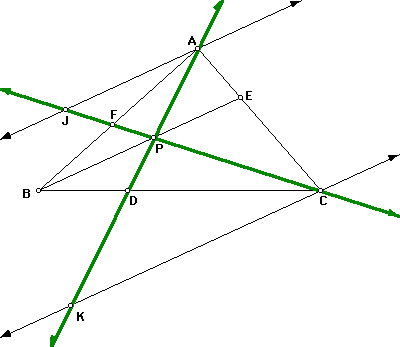 Figure 2: Extended lines.
These extended lines in addition to the parallel lines help to create multiple similar triangles.
Figure 3, Figure 4, and Figure 5 show the data that comes from the multiple similar triangles.
Figure 2: Extended lines.
These extended lines in addition to the parallel lines help to create multiple similar triangles.
Figure 3, Figure 4, and Figure 5 show the data that comes from the multiple similar triangles.
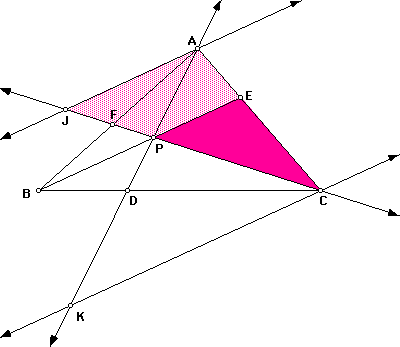 Figure 3: DAJC is similar to DEPC (by AA).
Figure 3: DAJC is similar to DEPC (by AA).
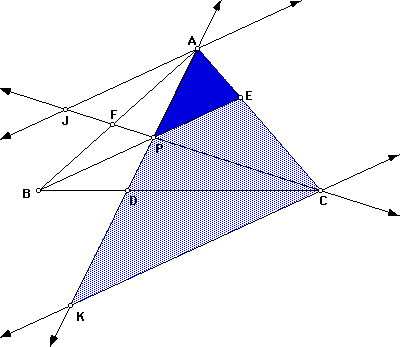 Figure 4: DAPE is similar to DAKC (by AA).
Figure 4: DAPE is similar to DAKC (by AA).
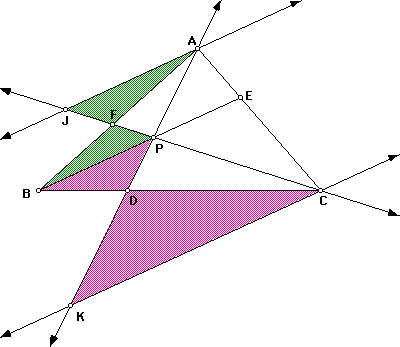 Figure 5:
DAFJ is similar to DBFP (by AA). DPDB is similar to DKDC (by AA).
Figure 5:
DAFJ is similar to DBFP (by AA). DPDB is similar to DKDC (by AA).
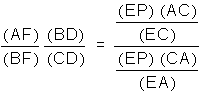 .
This simplifies to
.
This simplifies to
Return to Nicole's Page