. 
, the rotation
of by
radians.
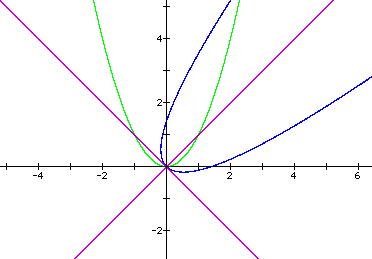
How did we get the formulas 
and 
? If we assume that
the green parabola is graphed in the xy plane (whose axes are the black
numbered axes above) and the blue graph is the equation graphed in the x'y'
plane (whose axes is the purple one above) then we can use the matrix 
to
rotate the xy (black graph coordinate system to the x'y' coordinate system.
To rotate an object one might just rotate each coordinate. So if we consider
xy the coordinate system in which we are working and we would like to rotate
the point (x,y) by 
radians in the clockwise direction to (x',y') as in
the diagram below.
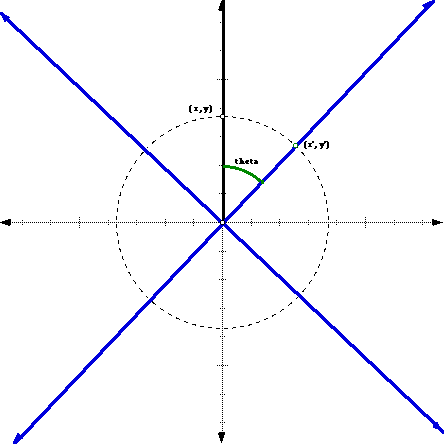
Now if we would like to write the point (x, y) in terms of the x'y' axes.
Then we can write the point (x,y) using unit vectors in both coordinate
systems
and if multiply both sides of the equation by
1. 
the resulting equation is 
2. 
the resulting equation is 
.
We take the dot product of each pair of vectors using the formula 
,
and use appropriate trigonometric identities to see that
1. and
2. as desired!