The Gergonne Point, so named after the French mathematician Joseph Gergonne, is the point of concurrency which results from connecting the vertices of a triangle to the opposite points of tangency of the triangle's incircle. This essay will prove the existence of this point for any triangle, explore its relationship to the Euler line, if any exist, and discuss the possible usefulness of this point.
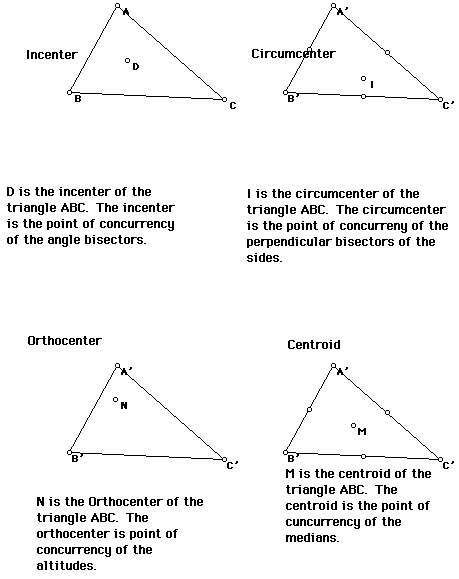
Most geometry students are familiar with the several points of concurrency and the steps necessary to construct such points. These might include some of the following points of concurrency (click for a GSP sketch illustration):
1. perpendicular bisector point of concurrency (circumcenter)
2. angle bisector point of concurrency (incenter)
3. median point of concurrency (centroid)
4. altitude point of concurrency (orthocenter)
An illustration of these below:

A GSP sketch of the Gergonne Point is shown below.
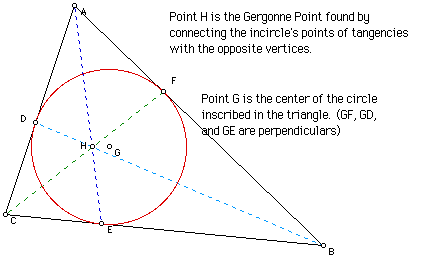
A key question that might be raised by students is whether
this point of concurrency occurs for any shape of triangle. Click here for a GSP sketch in which a randomly
formed triangle can be examined by using the selection tool to move the
vertices to change the shape.
Now that it has been shown visually that the Gergonne Point
may be found for any triangle, it might be of value to prove this points
existence through the use of the Segment Addition Postulate, which says
that B is between A and C if AB + BC = AC. This time a GSP sketch can be
examined with a corresponding table of values which demonstrate that the
Gergonne Point H is between each segment that connects the vertices to the
incenter's points of tangencies. For a GSP sketch, click
here to see Segment Addition for the Gergonne Point. Now that it
has been shown that the point B is between the other two points on each
segment and that the point is on all three segments at the same time, then
it must be a point of concurrency for all three segments. Note: This is
a very informal way to illustrate concurrency - go to the next section for
more rigor using Ceva's Theorem.
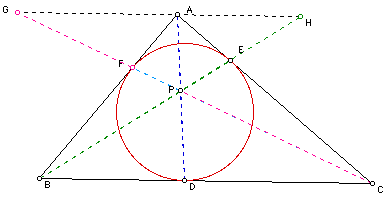
According to Ceva's Theorem, in a triangle ABC, three lines AD, BE, and CF intersect at a single point P if and only if AE/EC * CD/DB * BF/FA =1
The proof flows as follows:
PART 1 In a triangle ABC, if three lines AD, BE, and CF intersect at a single point P, then AE/EC * CD/DB/ * BF/FA = 1
Extend the lines BE and CF beyond the triangle until they meet GH, the line through A parallel to BC. There are several pairs of similar triangles including AHE and BCE, AFG and BCF, AGP and CDP, and finally BDP and AHP. These can be shown similar through alternate interior angles and vertical angles which lead to AA Similarity (see figure below).

From the similar triangles these proportional sides are derived:
1. AE/EC = AH/BC
2. BF/FA = CB/AG
3. AG/CD = AP/DP
4. AH/DB = AP/DP
The last two (#3 and 4) are both linked by AP/DP which yields AG/CD = AH/DB. This proportion is the same as CD/DB = AG/AH. The product of this with the first two gives AE/EC * CD/DB/ * BF/FA = AH/BC*AG/AH*CB/AG which leads to (AH*AG*CB)/(BC*AH*AG) =1. Therefore, if the lines AD, BE, and CF intersect in a single point P, the identity equaling 1 has been proven.
PART 2 In a triangle ABC, if AE/EC * CD/DB * BF/FA = 1, then the three lines intersect at a single point P.
Assume that there are at least two points of intersection between the lines.This implies that P and a P' can be the point of intersection of BE and CF and AD; next draw the line AP' until its intersection with BC at a point D' (possible if there are two points of concurrency). Then, from the previously proven part one above, it follows that AE/EC*CD'/D'B*FB/AF=1.
Will a point D' be the same as D?

Also, it has been specifically shown from part one that
AE/EC * CD/DB * BF/FA=1. Combining the two yields CD'/D'B=CD/DB or CD'/D'B
+ 1 = CD/DB +1; these lead to (CD'+D'B)/D'B = (CD+DB)/DB. Finally, by segment
addition, CB/D'B = CB/DB which implies that D'B=DB. Thus D' and D have to
be the same point which contradicts the assumption that there could be two
distinct points of concurrency.
Another approach to showing the existence of the Gergonne
Point is to use GSP to create axes and a grid in order to examine the three
linear equations that could be formed from making segments that join the
vertices of each triangle to the points of concurrency of the incenter to
each side. These linear equations might be explored on software such as
Algebra Xpressor. The point of intersection of the three lines should be
the ordered pair solution to the system of equations which would indicate
the existence of the Gergonne Point.
A possible relationship to the Euler Line can now be explored fro the Gergonne Point. The following GSP sketch illustrates the Euler Line.
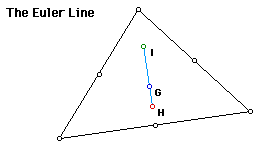
The Euler Line is the result of connecting the point of concurrency of the orthocenter, centroid, and circumcenter. The following sketch shows the Euler Line with the Gergonne Point.
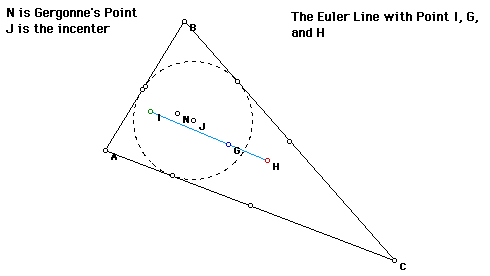
Although there does not seem to be any special theories concerning the Gergonne point itself, the point can be examined in regard to certain ratios of triangles created by the inscribed circle of the incenter.
Notice the relationship of the triangles in the figure and the greater than or equal to 4 ratio.
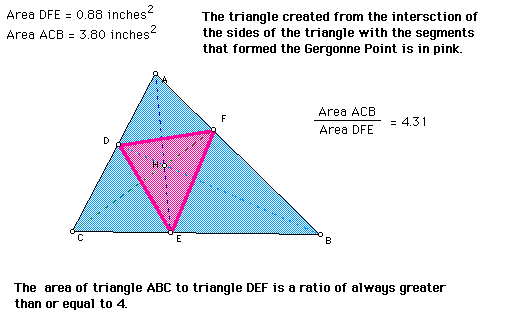
Can you prove this for any triangle? Can you find any other special qualities of the Gergonne Point?