

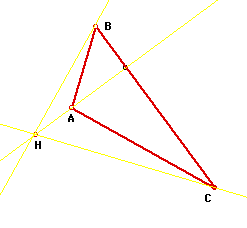
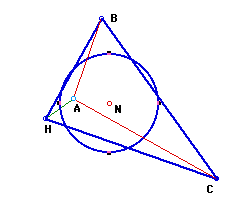
The Nine-Point circle for any triangle passes through the three
mid-points of the sides, the three feet of the altitudes, and
the three mid-points of the segments from the respective vertices
to the orthocenter. Thus, we have the Nine-Point circle (with
center N) of triangle ABC.
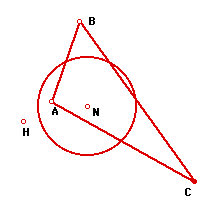
Next, let's overlay the Nine-Point circle of triangle HAB.
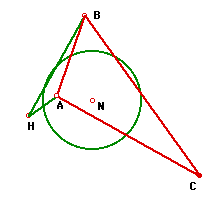
WOW! It's the same circle. Why?
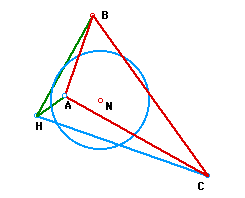
Again, it is the same circle. Why?
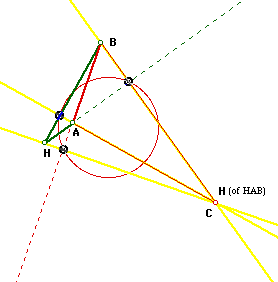
The question, "WHY?", can be answered by looking at the construction of the Nine-Point circle of each triangle.
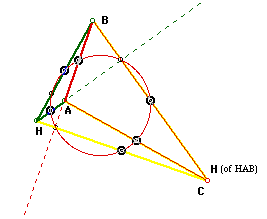
Thus we have the first three points. Notice that the same three point are the feet of the altitudes of triangle ABC. Starting at the top point and moving couterclockwise, we see that he first point is the intersection of the altitude from vertex A to side BC. The next point starts at vertex B and intersects the line containing side AC, and the third point originates at vertex C and intersects the extended side AB.
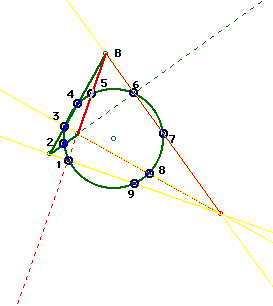
Again, notice the relationship between these points and the
same six points of triangle ABC. Sides HA and HB of triangle HAB
are the segments from vertices A and B, respectively, to the orthocenter
of triangle ABC. Side AB is shared by the two triangles. Sides
AC and BC of triangle ABC are the segments from vertices A and
B, respectively, to the orthocenter of triangle HAB. Finally,
side HC is the segment from vertex H to the orthocenter of triangle
HAB, and it is the segment from vertex C to the orthocenter of
triangle ABC.
Hence the midpoints of the segments are common to both triangle
ABC and triangle HAB.
Similar comparisons can be made with triangles HAC and HBC
to show why their Nine-Point circles are the same as the circles
of triangle ABC or of triangle HAB.
Return to Philippa's EMT Homepage