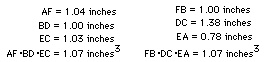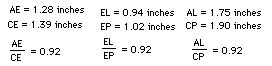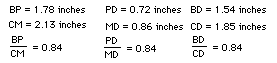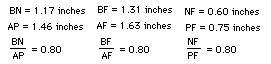Bill Tankersley's EMT 668 Page
Final Project - Part 1
Problems 2 and 3
Problem 2
Problem 2: You are given a rectangular sheet of cardboard measuring
15 inches by 25 inches. If a small square of the same size is cut from each
corner of the rectangle and each side is folded up along the cuts to form
a lidless box,
a) What is the maximum volume of the box?, and
b)What size(s) of the square would produce a box of volume equal to 400
cubic inches?
Solutions
1. Using Algebra XPresser:
After making a sketch of the rectangle on paper, we can determine the dimensions
of the box. If we let x represent the length of one side of the square that
we cut from each corner of the rectangle, then the expressions 15-2x and
25-2x represent the width and length, respectively, of the rectangle. Therefore,
the volume of the box is equal to height*length*width, or expressing volume
(V) as a function of x, we get:
V(x) =x*(15-2x)*(25-2x).
First, let's take a look at the graph of the volume function, which is an
upside down parabola. The values along the x-axis are values in inches,
whereas the values along the volume axis, or y-axis, are values in cubic
inches:
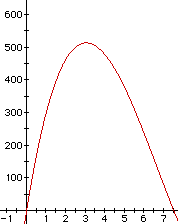
Now, if we zoom up on the maximum point of the parabola, we will be
able to answer question a, which is: What is the maximum volume of the box?
From the graph above, it looks like the maximum value is somewhere near
500 cubic inches. Here is a close-up view of the maximum point of the graph
above:
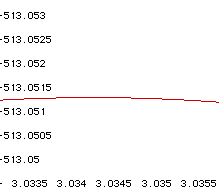
It appears as if the maximum volume of the box is approximately 513.0513
cubic inches, which occurs when the length of the square in each corner
of the original rectangle is approximately 3.03425 inches in length.
Now, let's answer question b, which is: What size(s) of the square would
produce a box of volume equal to 400 cubic inches? To answer this, I decided
to overlay a graph of the line V=400 (in green), and find the intersection(s).
Here is a close-up look at the graph:
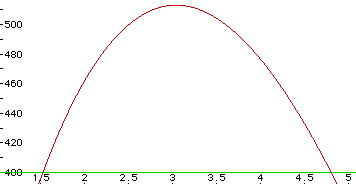
From the graph, we can see that when x takes on the approximate values
1.52 inches and 4.8 inches, the volume of the box reaches the desired measurement
of 400 cubic inches. So, there are indeed two lengths of x that will give
the desired volume measurement.
2. Using a Microsoft Excel Spreadsheet:
Click here to open a Microsoft Excel spreadsheet to
examine and test the data for the box problem. From the spreadsheet, we
get a more accurate approximation of the maximum volume of the box and the
two lengths of x that produce a box of volume 400 cubic inches. Using the
height, width, and length of the box expressed in terms of x as discussed
in the solution above, we can enter these expressions in the spreadsheet
cells. Again, we see that the maximum volume of the box is approximately
513.051 cubic inches when x is approximately 3.03425 inches. Also, the values
of x that produce a box with volume 400 cubic inches are approximately 1.5249
inches and 4.7928 inches. To better show the maximum volume, I included
values for x of 3.02 inches and 3.04 inches. Notice that the volume of the
box as x takes on these two values falls below that of the maximum.
3. Using GSP:
GSP provides a dynamic environment in which to explore the box problem.
First, we construct a segment of length x, which is used as the height of
the box. Then, we construct a box with scale factors of 15-2x for the width
and 25-2x for the length. Using the animate feature, we can change the length
of x while watching the volume of the box change. This solution gives the
same exact values for the maximum volume and length of x when the volume
is 400 cubic inches as the previous two solutions. Here is the box layout
from the GSP sketch for the box problem:
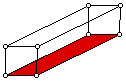
In the GSP file, you can animate segment EF, which is the length the
side of a square cut from the corner of the original rectangle. The solution
here matches the solutions found using Algebra XPresser and Excel.
Click here to download the GSP file for the box problem.
End of Problem 2
Problem 3
Problem 3: Consider any triangle ABC. Select a point P inside the triangle
and draw lines AP, BP, and CP extended to their intersections with the opposite
sides in points D, E, and F, respectively:
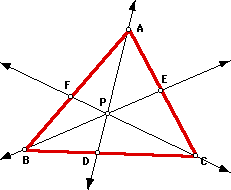
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various
locations of P. Conjecture? Proof? Also consider the ratio (AF)(BD)(EC)/(FB)(DC)(EA).
Can the result be generalized so that point P can be outside the triangle?
Click here to download the GSP file for the
sketch above.
To get started, I first measured each of the line segments above for many
triangles and various locations of P, and I came to the conclusion that:
(AF)(BD)(CE) = (FB)(DC)(EA)
for any triangle, as long as point P is inside the triangle. When point
P is outside the triangle, we lose 4 of the 6 segments. When measuring the
segments for many different triangles and various locations of P, the relationship
stated above always held true, as is pictured in the following set of measurements:
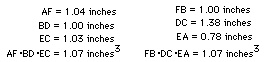
Since this is always the case, we can say without a doubt that:
(AF)(BD)(CE)/(FB)(DC)(EA)=1.
Now, the difficult part is proving this conjecture. To do so, I drew some
parallel lines and found similar triangles. Here is the drawing above with
the addition of the needed parallel lines:
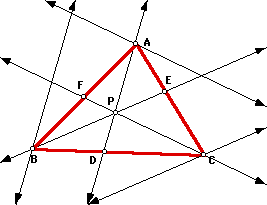
What we see immediately above is that each of the 3 original lines that
pass through point P have another line that is parallel to each of them.
Now, we need to label intersections and try to find similar triangles:
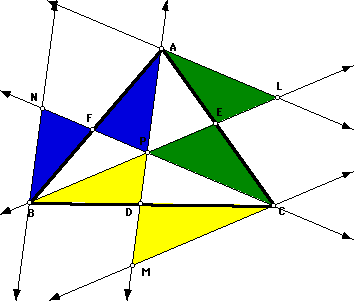
Now, after labeling intersections and color-coding suspected similar triangles,
it needs to be proven that the triangles colored alike are similar. Here
are measurements taken from the above drawing.
1. (Green) Triangle AEL is similar to triangle CEP:
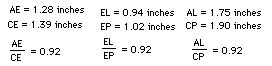
2. (Yellow) Triangle BPD is similar to triangle CMD:
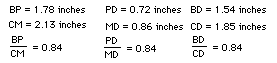
3. (Blue) Triangle BNF is similar to triangle APF:
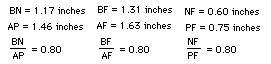
We know that our claims of similarity are correct, since the sides of
each pair of triangles are in equal proportion.
Now, this similarity establishes the following for each triangle ABC tested:
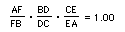
Therefore, we can claim that: (AF)(BD)(EC)/(FB)(DC)(EA)=1, which leads
to the next claim, which is: (AF)(BD)(EC) = (FB)(DC)(EA) .
End of Problem 3
End of Part 1