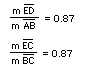Department of Mathematics Education
EMT 669, J. Wilson
An Essay on Triangles of Medians
Let's first examine the meaning of the term triangle of medians. Shown
below is triangle ABC with its three medians (segments AD, BF, and DC).
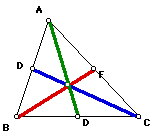
Now, we construct a triangle DEC (the triangle of medians) whose sides
are the medians of triangle ABC:

As one of the write-ups for EMT 668 (fall 97), I was trying to
find some relationship between a triangle and its triangle of medians. What
I discovered is that the ratio of their areas is a constant, which is 3/4.
To further examine this investigation, click
here.
I am still interested in investigations regarding a triangle and its triangle
of medians. Therefore, I chose to write an essay for EMT 669 centered around
the following:
Problems
1)Will an isosceles orginal triangle generate an isosceles triangle of medians?
2)Will a right triangle always generate a right triangle of medians?
3)What if the medians triangle is a right triangle?
4)Under what conditions will the original triangle and the medians triangle
both be right triangles?
To see a GSP file of a triangle (ABC) and its triangle of medians
(CED), click here. You will be able to click and
drag on a vertex of triangle ABC and determine the results for yourself.
Our first investigation is to answer question 1 above. That is,
will an isosceles original triangle generate an isosceles triangle of medians?
Shown below are two isosceles triangles (ABC) and their resulting triangle
of medians (CED):

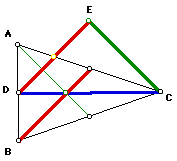
In both examples, we find that the medians triangle is also iscosceles.
This makes sense in that an isosceles triangle will have two medians that
are congruent, which happen to be the two medians to the two congruent sides.
Next, we will investigate question 2 above, which is: Will a right
triangle always generate a right triangle of medians? Here are three right
triangles (ABC) and their triangle of medians (CED):
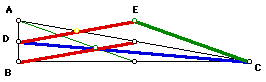

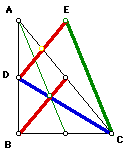
The result we see here is that it is possible for a right triangle
to generate an acute, right, or an obtuse triangle of medians.
Now it is time for question 3, which is: What if the medians triangle
is a right triangle? Here are three median triangles (CED) with their original
triangle (ABC):
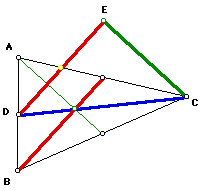


The result we see here is that a right triangle of medians can have an
acute, obtuse, or right original triangle.
Question 4: Under what conditions will the original triangle and
the medians triangle both be right triangles?
This is the same situation as pictured in the third example immediately
above. After some experimentation here, I noticed that the following ratios
held:

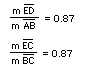
My conjecture here is that the original triangle and the medians triangle
will both be right triangles if the above ratios are equal, as pictured.
Click here to test the conjecture for yourself.
Return to Bill's EMT 669 class page