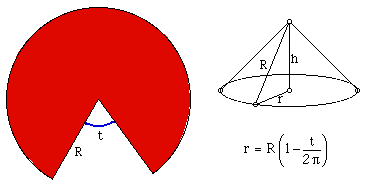
Click here for a problem description
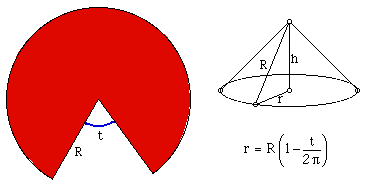
Our objective is to find the value of t for which the volume of the resulting cone is a maximum. While this is a pretty standard Calculus problem - the challenge is to see if we can do it without Calculus and use the AM- GM inequality
That ![]() follows fairly easily from the structure of the problem.
follows fairly easily from the structure of the problem.
![]() . By Pythagoras
. By Pythagoras ![]() which leads us to
which leads us to ![]() .
.
Hence: 
Then by the AM- GM inequality: ![]() with equality iff:
with equality iff: ![]()
[Note: This use of the A.M.-G.M. inequality does not give us a function on the Right Hand Side of the inequality that is a constant. Therefore, even though we can find a value of x for which the two functions are tangent at that point, we can not argue that the function on the RHS is larger for all values of x.]
It follows that: ![]() and
and ![]()
The maximum volume is given by: ![]()
The value of t for which the volume is a maximum is: ![]()