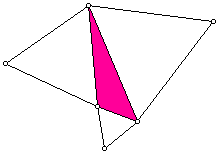
The very best (and easiest to follow) proof of why the Napoleon triangle
is equilateral that I could find was one offered by J.F. Rigby:

Using a triangle with equilateral triangles constructed on each side
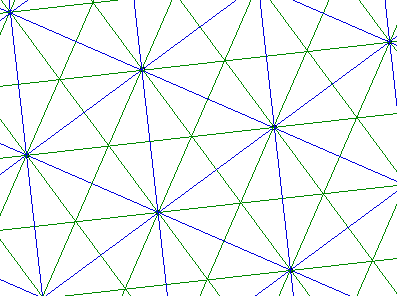
we can tesselate the plane.

We can now mark the centroids of the small equilateral triangles and
construct a triangular grid with these points.

Using these same points we can construct another triangular grid:
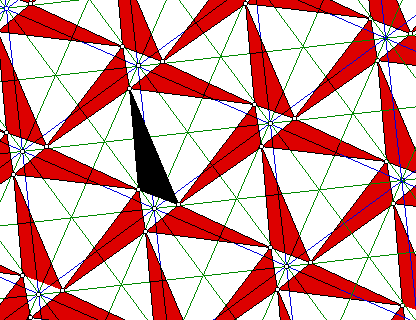
And we notice that the intersections of the green grid are the centroids
of the other equilateral triangles since Napoleon's triangle joins intersections
of the green grid it must be equilateral.
To play with a GSP sketch and observe the illustration for different
original triangles click here.