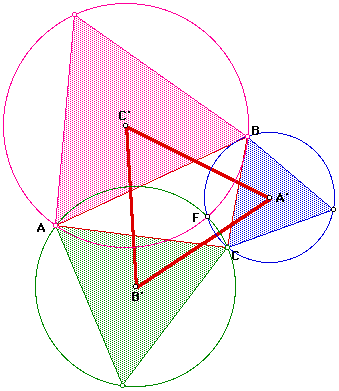
Napoleon's Triangle
Given a triangle ABC we can construct equilateral triangles on the outsides
of the triangle. The circumcircles of these triangles meet in a point called
the Fermat point and the centres of the circumcircles
form a fourth equilateral triangle -- the Napoleon triangle.
It is also interesting to note that the centroid of the Napoleon triangle
is the centroid of the original triangle.
To watch the Napolean triangle in a GSP sketch click
here.
For a discussion on why the Napoleon triangle is equilateral click
here.
Back

