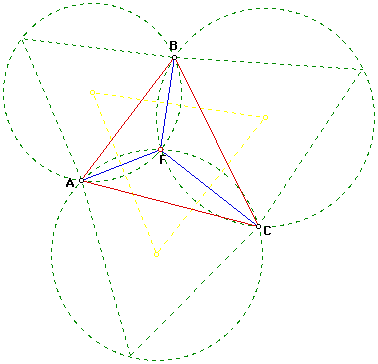
The Fermat point (F) is the point inside a triangle ABC (provided no
angle exceeds 120 degrees) such that the sum AF + BF + CF is a minimum.
According to a theorem (generally attributed to Napoleon Bonaparte), the
circumcircles of equilateral triangle constructed on the outside of triangle
ABC meet at the Fermat point and their centres form a fourth equilateral
triangle - the Napoleon Triangle.

For a discussion on the existence of this Fermat point click below:
1. Discussion on the intersection of the circumcircles,
2. Discussion illustrating that AF + BF
+ CF is a minimum.