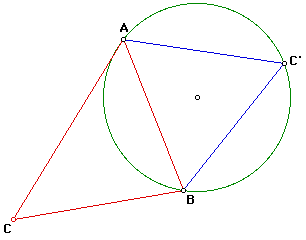

Consider triangle ABC and construct an equilateral triangle on segment AB, next construct the circumcircle of triangle ABC'. Segment AB divides the circle into two arcs - and subtends supplementary angles in the opposite segments ie angle ABC'' is 120deg.
Click here for a GSP animation of
C'' moving along arc AC''B.
In a similar way we can construct an equilateral triangle on AC, and construct
its circumcircle.
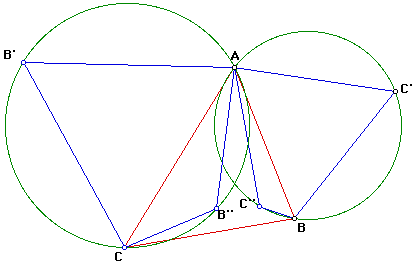
Click here for a GSP animation of
C'' movilg along arc AC''B and B'' moving along arc AB''C.
It is obvious that the two circles through A will intersect in only one
other point (at least I hope that is obvious to the reader) this will be
inside the triangle if angle CAB is less than 120deg and outside the triangle
if angle CAB is greater than 120deg (click
here for a GSP animation of this remark).
At the point of intersection of the two circles (say F) angle AFB and angle
AFC will both be 120deg so angle CFB will also be 120deg and it follows
that the circumcircle of an equilateral triangle on segment CB will also
pass through F!
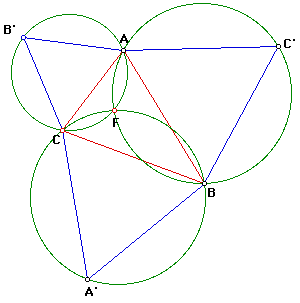
It remains to show that this point is such that the sum AF + BF + CF
is a minimum. This is best illustrated by another
discussion (click here).