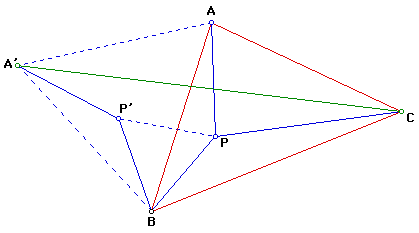
This proof (by Coxeter) involves reflections.
Consider first an arbitrary point P inside the triangle. Join it to A, B
and C and rotate the inner triangle APB through 60deg about B to obtain
A'P'B with ABA'' and PBP' equilateral triangles.

Now AP + BP + CP = A'P' + P'P + PC which is a path from A' to C. Such a path is minimal when it is a straight line - ie when P' and P lie on A'C.
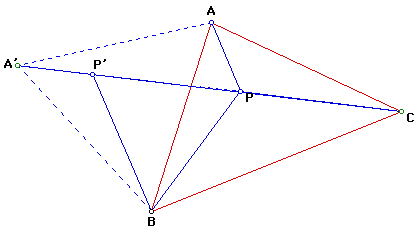
This occurs when angle BPC = 180 - 60 (angle BPP') = 120deg.
It follows that the sum AP + BP + CP is a minimum at a point (P) for which
the three sides subtend an angle of 120deg - the intersection of the circumcircles
of equilateral triangles subtended on the oustide of triangle ABC - a remark
best illustrated by another discussion (click
here).