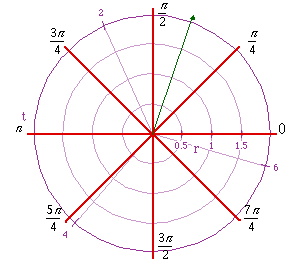

When plotting co-ordinates (r, t) in the polar plane r represents the
distance of the point from the origin along a line (say the green line)
that has moved anti-clockwise for a time t (though for our purposes it is
more useful to think of this as an angle t).
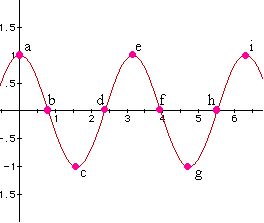
Let us now consider the graph of y = cos x drawn on a rectangular plane
(a graph with which I am assuming the reader is familiar):

I have marked the critical points of the graph so that we can see what
happens to these points as we plot the same graph in polar coordinates.
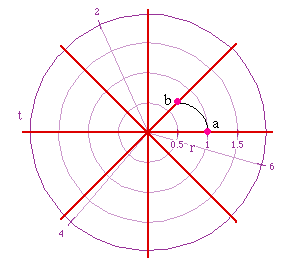
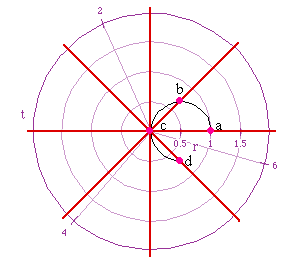
It is a good idea to pause for a moment and be sure that we understand
why the shape of the curve is what it is from c to d. If we look at the
curve of y = cos x we notice that cos x is negative for pi/2 < x <
3 pi/4 how does that translate on this graph? In the case of point d we
can think of the green line (in the earlier figure) having rotated through
3 pi/4 and the value of r (in r = cos(t)) will be negative so we plot the
point d on the green line, extended through the origin, and on the opposite
side of the origin on the line.
STOP and be sure that you understand this explanation before you continue
with this paper - this is a vital concept.
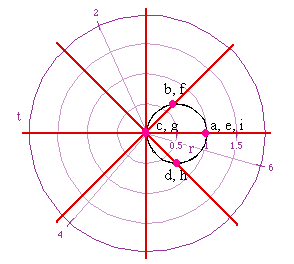
Finally compare this graph with that of y = cos x (in rectangular co-ordinates)
-- if you understand the labeling of this graph we are ready to proceed.
So what will happen with y = cos 2 x and r = cos 2 t
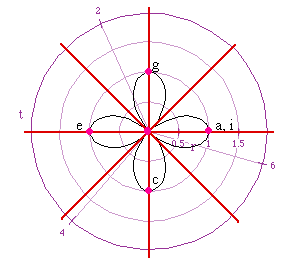
We are now ready to explore the full range of graphs r = a + b cos (k
t). From here on we will not draw the graphs with rectangular co-ordinates
again -- the reader is encouraged to draw these themselves to ensure that
they understand the graphs properly.
(i) the role of the variable k in r = a + b cos (k t)
r = cos (4 t) r
= cos (6 t) r = cos (3 t)
So what about fractions......
r = cos (0.5 t) r
= cos (1.5 t) r = cos (2.5 t) r
= cos ((2/3) t) r = cos ((4/3) t)
It seems quite obvious that k plays the same role in the polar equation
as it does in the rectangular co-ordinate system - ie it determines the
number of "leaves" (compare with cycles). For k an even number
the number of leaves equals 2k while for k odd the number of leaves equals
k (since the leaves lie "on top of each other").
(ii) the role of the variable b in r = a + b cos (k t)
r = 0.5 cos (2 t) r
= 1.5 cos (2 t) r = 2.0 cos (2 t)
It again seems quite clear that b has much the same effect in the polar
graphs as it does in the rectangular co-ordinates -- namely it changes the
"amplitude" of the graph.
(iii) the role of the variable a in r = a + b cos (k t)
r = 0.5 + cos (2 t) r
= 1 + cos (2 t) r = 1.5 + cos (2 t)
r = - 0.5 + cos (2 t)
While it is possible to anticipate the shape of these polar graphs based
on our observations so far -- it is harder to explain the change in shape
as being the result of the vertical shift of the cos graph.
(iv) r = a + b cos (k t)
r = 1 + 0.5 cos (2 t) r
= 0.5 + 0.5 cos (2 t) r = 1.5 + 0.5 cos
(2 t)
I hope that the reader will have noticed that the patterns we observe in
rectangular co-ordinates and graphs are comparable to those we observe in
polar-co-ordinates and graphs - quite a relief isn't it!!
Conclusion
I hope in this paper to have illustrated the power of exploring a new concept
in terms of familiar knowledge -- a valuable skill in Mathematics.
And finally the graph of: 0.5 + 1.5 cos (4 t):
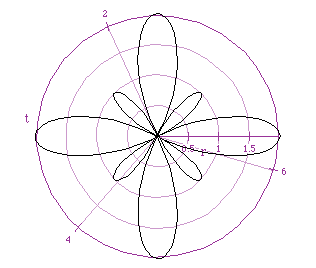
If you feel the need to test your understanding of this graph click
here.