Interesting questions indeed, n'est ce-pas? Keep an eye on figure 1 below. Notice the radius of this circle is 1; therefore, it is the unit circle.

FIGURE 1

This means that the arc AC is equal to the central angle ß. Line segment AC is less than arc AB. So, it follows segment AC < ß. Using the Pythagorean theorem together with this statement yields

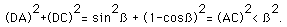
The terms here are positive, and since the parts are therefore smaller than the sum, we can write

Taking the square roots, we have |sinß|<|ß| and |1-cosß|<|ß|. It follows that -|ß|<sinß<|ß| and -|ß|<(1-cosß|<|ß|. What happens now if we take the limit as ß->0? We can see that sinß and 1-cosß are trapped between quantities approaching zero. Therefore, they themselves approach zero. Sinß and 1-cosß can be said to be effectively sandwiched between two quantities approaching zero. By analyzing as such, we are using the "sandwich theorem" to evaluate a limit. By the way, since 1-cosß is going to zero, then cosß is going to 1 as ß->0.

Now see if you can use our results to find these limits. Justify your answers.

1. Find the lim as x->0 of cotx.

2. Find the lim as x->0 of cscx.

Here is an interesting limit.

See if you can use a picture similar to figure 1 to prove this statement.

For help, click "prove it". Animate and study the picture. Read the question for each step. Use the "shows" to help you as necessary.

To return to the homepage, click " loondog".