

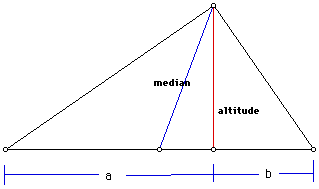
Take a right triangle and let its altitude from the right angle divide the hypotenuse into parts of lengths a and b. Interpret the comparison of the lengths of the altitude and the median from the 90 degree vertex of a right triangle having hypotenuse of length a+b.
Clearly, the length of the median is always greater than or equal to the length of the altitude. Express the lengths of median and the altitude in terms of a and b.
Conclusion? _______________________________
Hints/Solution:
Extensions/Variations:
Consider the triangles inscribed in a semicircle with one side formed by the diameter.
Reference: