

Let ABC be a triangle. Let AX be the bisector of angle A, and let CZ be the bisector of angle C. Let I be the intersection of AX and CZ.
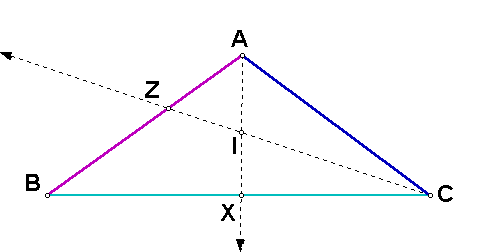
Construct the line through I perpendicular to segment AC. Construct the intersection of this line and segment AC, and label it E. Construct the line through I perpendicular to segment BC. Construct the intersection of this line and segment BC, and label it F. Construct the segment OC.
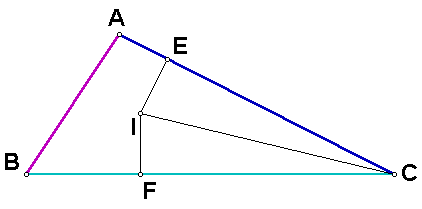
Consider triangles ICF and ICE. Angles IFC and IEC are both right angles, so they are congruent. Angles ICF and ICE are congruent because IC bisectors angle C. Since the sum of the interior angles of a triangle is 180 degrees, and two angles of the two triangles are congruent, the third angles of the triangles (angles FIC and EIC) are also congruent. Segment IC is congruent to itself, so triangles ICF and ICE are congruent by Angle-Side-Angle congruence.
Since the two triangles are congruent, segments IE and IF are congruent.
Construct the line through I perpendicular to the segment AB. Construct the intersection of this line and segment AB, and label is G. A similar process can be used to show that segments IG and IE are congruent.
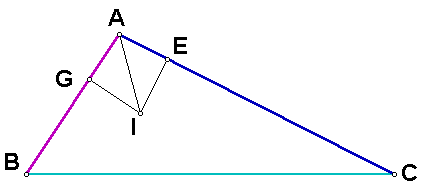
Therefore, segments IG and IF are congruent by transitivity.
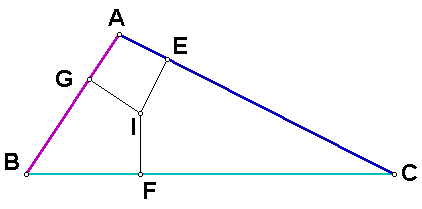
Now construct segment BI. If segment BI bisects angle B, then we will have shown that the three angle bisectors are concurrent.
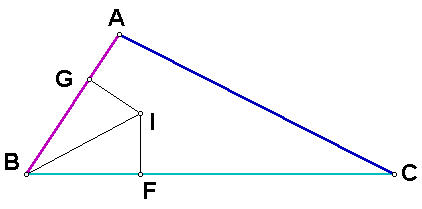
Consider triangles BIG and BIF. We have from above that segments IG and IF are congruent. Also, segment IB is congruent to itself. Since angles BGI and BFI are right angles, the Pythagorean theorem can be applied to the two triangles to show that segments BG and BF are congruent. Therefore, triangles BIG and BIF are congruent by Side-Side-Side congruence.
By the definition of congruent triangles, we now have that angles IBG and IBF are congruent. Therefore, segment BI bisects angle B. Thus, the three angle bisectors of the internal angles of the triangle are concurrent -- they all go through the point I. 