

Click here to verify the theorem using GSP.
Let C be a circle with center O, and let <XYZ be an acute angle that is inscribed in circle C.
Construct segments XZ and OY.
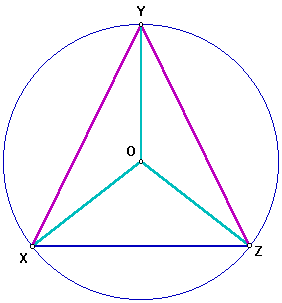
Segments OX, OZ, and OY are radii of the circle, so they are congruent. Therefore, triangles OXZ, OYZ, and OXY are isosceles triangles. Since base angles of an isosceles triangle are congruent, we have
Label the angles as follows:
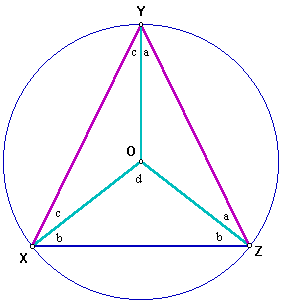
First consider triangle OXZ. Using the fact that the sum of the measures of the interior angles of a triangle is 180 degrees, we have
Considering triangle XYZ, we have
Since d = 180 - 2b and 2a + 2c = 180 - 2b, we can now write
Therefore, the measure of the inscribed angle (<XYZ) is equal to half the measure of the central angle (<XOZ). 