

Suppose ABC is any triangle. If P is any point in the plane, then the pedal triangle is triangle RST, where R, S, and T are the intersection points of the sides of ABC (extended if necessary) and the lines through P perpendicular to the sides of ABC (extended if necessary). The point P is called the pedal point.
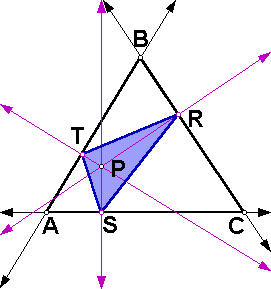
Click here for a GSP sketch of a triangle ABC with its pedal triangle RST and pedal point P.
Click here for a GSP script for the construction
What if P is the circumcenter of triangle ABC?
In the sketch below, C* is the circumcenter of the triangle ABC, and triangle RST is the pedal triangle with pedal point C*. The pedal triangle appears to be the same as the medial triangle for triangle ABC, but let's investigate.
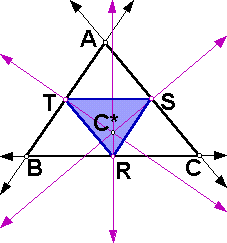
Click here for a GSP sketch of the above.
Theorem: The pedal triangle RST of a triangle ABC with pedal point C*, the circumcenter of triangle ABC, is the medial triangle of triangle ABC.
Proof: Since C* is the circumcenter of triangle
ABC, we know that C* is on the perpendicular bisector of BC. Since there
is only one line through C* perpendicular to BC, and C* is on the perpendicular
bisector of BC, any line through the point C* that is perpendicular to BC must
be the perpendicular bisector of BC. From the construction of the
pedal triangle, we know that the line C*R is perpendicular to line BC, so C*R
must be the perpendicular bisector of BC. Therefore, since C*R bisects BC,
R is the midpoint of BC. Similarly, S is the midpoint of AC, and T is the
midpoint of AB. Thus, since the medial triangle of a triangle is the
triangle formed by joining the midpoints of the sides of the triangle, triangle
RST is the medial triangle of triangle ABC.![]()
This proof works regardless of whether C* is inside, on, or outside triangle ABC.
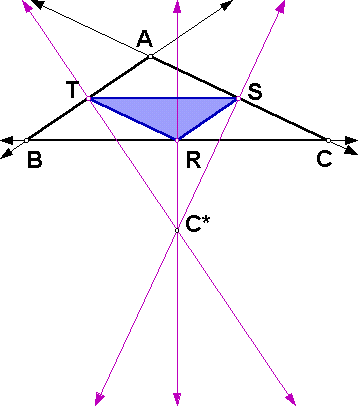
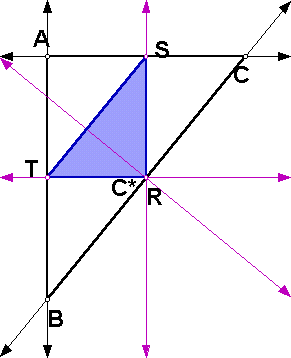
Since R, S, and T are the midpoints of triangle ABC, we can make some interesting conclusions about triangle RST.
Theorem: Given any triangle ABC, let R be the midpoint of BC, S be the midpoint of AC, and T be the midpoint of AB. The medians RS, ST, and TR are half the length of and parallel to sides AB, BC, and AC, respectively.
Proof: Let be a triangle ABC, let R be the midpoint of BC, let S be the midpoint of AC, and let T be the midpoint of AB. Since T is the midpoint of AB, AT = 1/2 AB. <TAS is congruent to < BAC because they are the same angle. Since S is the midpoint of AC, AS = 1/2 AC. Therefore, triangles ABC and ATS are similar triangles with similarity ratio 1/2. Therefore, the length of TS is half the length of BC. Since ABC and ATS are similar, angles ATS and ABC are congruent. When two lines (TS and BC) are cut by a transversal (AB) so that corresponding angles are congruent, the two lines are parallel. Thus, TS is parallel to BC.
Similarly, triangles SRC and ABC are similar with similarity ratio 1/2, so RS = 1/2 AB and RS is parallel to AB.
Triangle BTR is similar to triangle ABC with similarity ratio
1/2, so TR = 1/2 AC and TR is parallel to AC.![]()
Theorem: Given any triangle ABC, let R be the midpoint of BC, S be the midpoint of AC, and T be the midpoint of AB. Then triangles TSA, BRT, and RCS are congruent.
Proof: From the previous proof, we have that
triangles TSA, BRT, and RCS are similar to triangle BCA with similarity ratio
1/2. Thus angles TAS, BTR, and RSC are congruent. We also know that
1/2 AB = AT = TB = SR, and angles ATS, TBR, and SRC are congruent.
Therefore, the three triangles are congruent by Angle-Side-Angle congruence.![]()
Theorem: Given any triangle ABC with medial triangle RST, triangles ABC and RST are similar with similarity ratio 1/2.
Proof: Since triangles BRT, and RCS are similar to
triangle BCA with similarity ratio 1/2 (see above), we know that RS = 1/2 AB and
RT = 1/2 AC. Since the sum of the measures of the interior angles of a
triangle is 180 degrees, we know that m<BAC = 180 - m<ABC - m<ACB.
From the fact that the triangles are similar, we also know that m<ACB = m<TRB
and m<ABC = m<SRC. So m<BAC = 180 - m<SRC -m<TRB = m<SRT,
since angles SRC, SRT and TRB for a straight-angle and the measure of a
straight-angle is 180 degrees. Therefore, triangles ABC and RST are
similar by Side-Angle-Side similarity, with similarity ratio 1/2.![]()
Theorem: Given any triangle ABC with medial triangle RST, the area of triangle RST is one fourth of the area of triangle ABC.
Proof: From the previous proofs, we know that
triangles ATS, TBR, SRC, and RST are similar to triangle ABC with similarity
ratio k. Thus, triangles ATS, TBR, SRC, and RST are congruent. Since
these four triangles make up triangle ABC, the area of each one is 1/4 the area
of triangle ABC. In particular, the area of triangle RST is 1/4 the area
of triangle ABC.![]()