Posed Problem:  Here is an interesting challenge. How to construct a circle that is tangential to two given circles, one of which is inside the other.

To understand the scenario better, let us call them BIG CIRCLE, SMALL CIRCLE and TANGENTIAL CIRCLE. The SMALL CIRCLE is inside the BIG CIRCLE and we have to construct the TANGENTIAL CIRCLE.

First of all, it is obvious that the TANGENTIAL CIRCLE is also going to be inside the BIG CIRCLE. If it is outside, then it won't be able to be tangential to the SMALL CIRCLE without intersecting the BIG CIRCLE.

Next, we also need to recognize that as we can place the SMALL CIRCLE anywhere inside the BIG CIRCLE, we probably will be able to construct more than one TANGENTIAL CIRCLE.  In fact, we will see that we are going to be able to construct what is called, a FAMILY of such TANGENTIAL CIRCLES.

We are now ready to go about the construction.  We begin this investigation by constructing two circles, BIG CIRCLE and SMALL CIRCLE. 

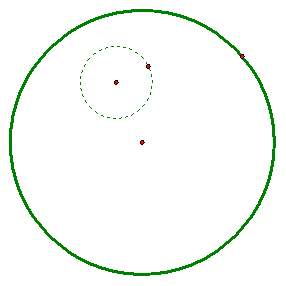
The next thing we did was to draw a line from the center of the BIG CIRCLE and let it intersect anywhere on the circumference of the BIG CIRCLE.  For convenience, let us ensure that such a line does not intersect the SMALL CIRCLE.

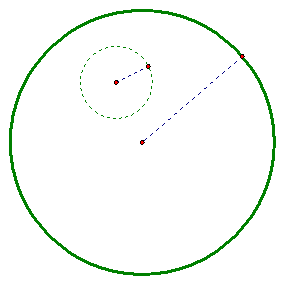
Next, using the radius of the SMALL CIRCLE and a point on the BIG CIRCLE, we constructed a circle by center on the BIG CIRCLE. 

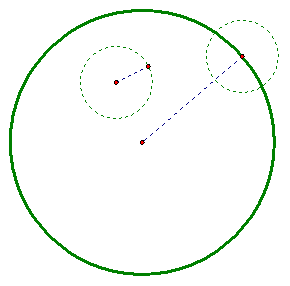
Next, we had to identify a point on the top of the newly constructed little circle. To do this, we extended the line through the center of the BIG CIRCLE that would pass through the new little circle.  We then constructed a line segment from the center of SMALL CIRCLE to the point on the new little circle.  

Next, we located the midpoint of the line segment formed between the SMALL CIRCLE and the new little circle.  A perpendicular line was then constructed through the midpoint.  This is our perpendicular bisector.

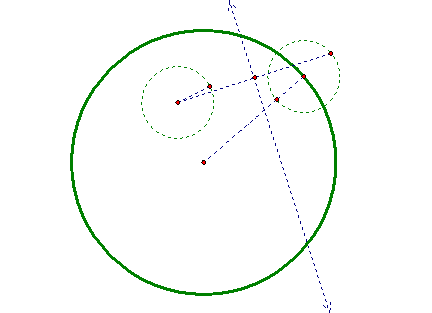
Next, as we know the center of the TANGENTIAL CIRCLE is going to be equidistant from this point and the center of the SMALL CIRCLE, we find the point of intersection of the perpendicular bisector of the the line joining this point and the center of the SMALL CIRCLE and the line that we drew from the center of the BIG CIRCLE to its circumference. This point of intersection is going to be the center of the TANGENTIAL CIRCLE.  This is the TANGENTIAL CIRCLE that we wanted. 

A couple of things to note, is that the centers of the BIG CIRCLE & the TANGENTIAL CIRCLE will be collinear.  Also, the distance from the center of the TANGENTIAL CIRCLE to the outside of the SMALL CIRCLE (point of tangency) PLUS the radius of the SMALL CIRCLE, is equal to the distance from the center of the TANGENTIAL CIRCLE to the point of tangency with the BIG CIRCLE PLUS the radius of the small circle. This is because the distance from the center of the TANGENTIAL CIRCLE to the two points of tangency (inside tangency of BIG CIRCLE and outside tangency of SMALL CIRCLE) will be the radius of the TANGENTIAL CIRCLE.

Now consider the following.  Suppose we construct a segment that joins the centers of the SMALL CIRCLE and the TANGENTIAL CIRCLE.  This segment is the sum of the radii of the TANGENTIAL CIRCLE and the SMALL CIRCLE.  We obtain the following.

Since we constructed a new little circle from the SMALL CIRCLE on the circumference of the BIG CIRCLE, the segment from the center of the BIG CIRCLE to the new little circle is the same measure.  And so, we have and isosceles triangle. 

We now want to consider the locus of the center of all such circles tangent to the two given circles.  We can animate the circle and trace the locus of the center.  Can you guess what the locus of the center of all circles tangent to two given circles will be.  Click here to open GSP -- then click on the ANIMATE POINT button and find out.

You guessed correct!  It is an ellipse. 

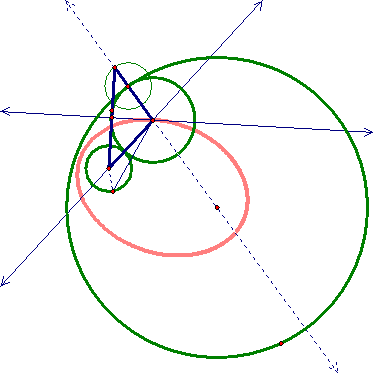
Now what happens when the given circle or the SMALL CIRCLE is outside of the BIG CIRCLE?  Well we still get an ellipse.  Also note that the distance between the foci is starting to increase.  

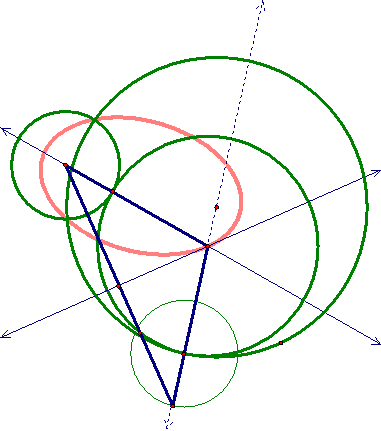
So, there are two things that we observed happening.  As we increase the distance of the foci, something is happening.  Also, as we move our SMALL CIRCLE outside of the BIG CIRCLE, something is also happening.  This looks like it is the limiting case.  Let's make a conjecture.  I think that this is the limiting case -- the locus of the centers maybe a hyperbola.  What do you think will this be the case?  Click here and find out. 

Return to DNB's homepage         Return to VRam's homepage