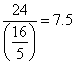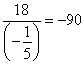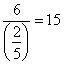Ken
Montgomery
EMAT 6690
MATHEMATICS
APPLIED IN INDUSTRY
Linear
Programming: The Simplex Method of Optimization
A company produces two types of product (Gadgets and Gizmos). The manufacturing process consists of assembly, polishing and packaging. The time required for each stage of manufacturing, for each product is given in Table 1.
|
Process |
Gadgets |
Gizmos |
Total Time Required |
|
Assembly |
2 |
4 |
36 |
|
Polishing |
3 |
1 |
36 |
|
Packaging |
5 |
2 |
30 |
|
|
|
|
|
|
Profit |
$30 |
$20 |
-
|
Table 1: Production Time Requirements
We let 
and
represent
the numbers of dozen Gadgets and Gizmos,
respectively and thus obtain the objective function (Equation 1) for
profit,
which we desire to maximize.
Equation
1: 
From table 1 we obtain the following production constraints.
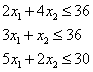
We also assume that production capability (parts, labor, etc.) will never be negative, so we have the following necessary constraints.
Applying the Simplex Method, we first use slack
variables 
,
and
to convert our constraint inequalities into constraint
equations. For example, since 
,
we know that if some amount, 
,
were added to the sum of
,
then 
.
The following constraint inequalities are thus obtained.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=30
We apply the Simplex Method by carrying out elementary row operations on a matrix, referred to as the simplex tableau. The simplex tableau is comprised of the augmented matrix corresponding to our system of constraint equations with the objective function coefficients in the form given by Equation 2.
Equation
2: 
The simplex tableau corresponding to our system of constraint equations and objective profit function is given in Tableau 1. The current z-value (profit) is zero and is located in the last row and the b-column (highlighted in red). This is the value to maximize.
|
|
|
|
|
|
b |
|
|
2 |
4 |
1 |
0 |
0 |
36 |
|
|
3 |
1 |
0 |
1 |
0 |
36 |
|
|
5 |
2 |
0 |
0 |
1 |
30 |
|
|
-30 |
-20 |
0 |
0 |
0 |
0 |
|
Tableau 1
The initial solution is given by Equation 3, which yields z = 0, from Equation 1.
Equation
3: 
Throughout the simplex method we will perform an optimality check by inspecting the bottom row of the tableau for negative entries. Once all entries of the bottom row are greater than or equal to zero, the optimal solution has been found. Since we have two negative entries in the bottom row of Tableau 1 (–30 and –20), our present profit (z = 0) is not optimal.
The next step of the simplex method
is called pivoting
and begins with the selection of the pivot. We locate the most
negative
entry in the bottom row (-30), which will correspond to the entering
column,
which is 
(highlighted
blue in Tableau 2 below). For identical negative
values, any tied value may be chosen. To select the corresponding row
of our pivot,
we calculate the ratio of b to
,
for each row (
and
).
The ratios are given in Table 2.
|
|
|
|
|
|
|
|
Table
2:
Ratios of b and 
values
Since the value 6 is the smallest non-negative
ratio,
is chosen as the departing row (yellow in Tableau 2).
The pivot is therefore the entry in the entering column
and the departing
row, which in this problem is the value 5 (green in Tableau 2).
Notice that
we have replaced 
with
.
|
|
|
|
|
|
b |
|
|
2 |
4 |
1 |
0 |
0 |
36 |
|
|
3 |
1 |
0 |
1 |
0 |
36 |
|
|
5 |
2 |
0 |
0 |
1 |
30 |
|
|
-30 |
-20 |
0 |
0 |
0 |
0 |
|
Tableau 2
The next step is to use elementary row operations until the pivot is equal to 1, and all other entries in the entering column are equal to 0, which completes the pivoting process and results in Tableau 3.
|
|
|
|
|
|
b |
|
|
0 |
16/5 |
1 |
0 |
-2/5 |
24 |
|
|
0 |
-1/5 |
0 |
1 |
-3/5 |
18 |
|
|
1 |
2/5 |
0 |
0 |
1/5 |
6 |
|
|
0 |
-8 |
0 |
0 |
6 |
180 |
|
Tableau 3
The preliminary solution is given by Equation 4, which yields z = 180, from Equation 1.
Equation
4: 
We conduct our second optimality check and
notice
that since the second (
)
entry of the bottom row is negative (-8) we do not yet have
an optimal solution. We therefore repeat the steps necessary for pivoting.
Our entering column will thus be
and
we again select the departing row by calculating
ratios of b to
,
for each row (
,
and
).
The ratios are given in Table 3.
|
|
|
|
|
|
|
|
Table
3:
Ratios of b and 
values
Since 7.5 is the least, non-negative value, 
will
be the departing row. Again, applying elementary
row operations until the pivot is 1 and all other values in the
entering
column are 0, we obtain Tableau 4.
|
|
|
|
|
|
b |
|
|
0 |
1 |
5/16 |
0 |
-1/8 |
15/2 |
|
|
0 |
0 |
1/16 |
1 |
-5/8 |
39/2 |
|
|
1 |
0 |
-1/8 |
0 |
3/20 |
3 |
|
|
0 |
0 |
5/2 |
0 |
5 |
240 |
|
Tableau 4
After conducting another optimality check, we find that Tableau 4 yields the final solution, given by Equation 5, since the bottom row entries are all either positive or equal to zero.
Equation
5: 
Substitution of the values from Equation 5 into Equation 1 yields validation of our z-value in Tableau 4 and is given by Equation 6.
Equation
6: 
Work through the above problem and compare your
solution to
the Appendix, which contains complete
row
operations from the initial simplex tableau to the final tableau
presented
above.
Return to EMAT 6690