
Ken Montgomery
EMAT 6690
INSTRUCTIONAL
UNIT: Distance, Area, and Volume
PERIMETER
Perimeter, the quintessential problem of farmers and fence-builders the world over, is the total distance around a polygon. The calculation of perimeter is relatively straightforward in that one must simply add all of the side lengths of the polygon. Consider the quadrilateral given in Figure 1.
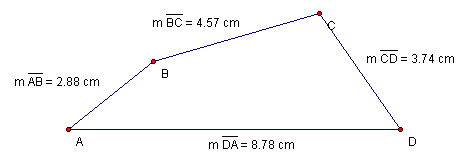
Figure 1: Quadrilateral ABCD
To find the perimeter of Quadrilateral ABCD, we simply add the lengths of the four sides (Equation 1).
Equation 1: ![]()
This definition may be applied to all n-gons (polygons with n sides) regardless of whether or not they are regular. A regular polygon has all sides congruent (of equal measure). However, in the case of regular polygons, the number of sides, n may be multiplied by the side-length. Consider the regular hexagon in Figure 2.

Figure 2: Regular Hexagon ABCDEF
Notice that we are only given one side-length, ![]() .
However, since Figure 5 is a regular hexagon, all six sides
are congruent, so we multiply the side-length by 6 to find the
perimeter
(Equation 2).
.
However, since Figure 5 is a regular hexagon, all six sides
are congruent, so we multiply the side-length by 6 to find the
perimeter
(Equation 2).
Equation 2: ![]()
Sometimes, both addition and multiplication may be used in calculating perimeter, such as in the case of parallelograms, which have two pairs of congruent, opposite sides (Figure 3).
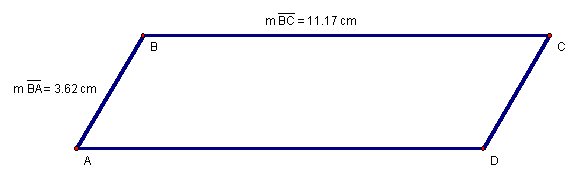
Figure 3: ![]() has
opposite sides congruent
has
opposite sides congruent
To find the distance around ![]() ,
we need only recognize that
,
we need only recognize that ![]() and
and![]() ,
thus the perimeter is given in Equation 3.
,
thus the perimeter is given in Equation 3.
Equation 3: ![]()
Circumference
Analogous to perimeter, for polygons, the distance around a circle is known as the circumference. The distance from the center of the circle to any point on the circle is called the radius. The radius is a constant value, since a circle, by definition, is a locus of points equidistant from a given point (the center). The diameter is twice the value of the radius (Equation 4).
Equation 4:![]()
The ratio of circumference to diameter is constant for any circle,
regardless of the size of the radius. This constant is known as pi,
represented by the Greek letter (![]() ),
and is approximated in the below relation.
),
and is approximated in the below relation.
![]()
By definition therefore, the value![]() is
equal to this ratio of circumference and diameter
(Equation 5).
is
equal to this ratio of circumference and diameter
(Equation 5).
Equation 5: ![]()
Multiplying both sides of the equation by d yields Equation 6.
Equation 6: ![]()
Substituting from Equation 4, we also have Equation 7.
Equation 7: ![]()
There are thus, two convenient formulas for circumference
calculation
depending upon whether the diameter or radius is indicated.
Return to EMAT 6690