

Problem 2.
Investigate this sequence for a range of x(0).
x(n+1) = 3.83[x(n)][ 1 - x(n)]
First, we evaluate the sequence for 0 and 1.
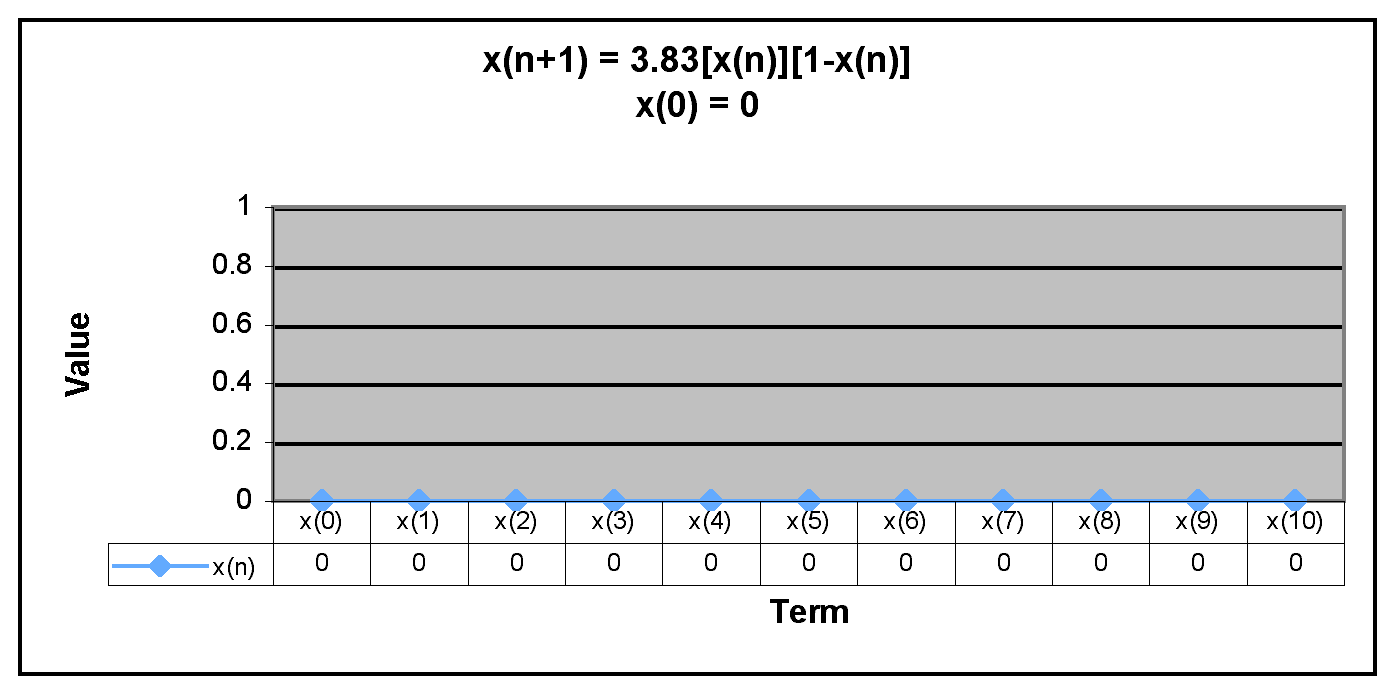
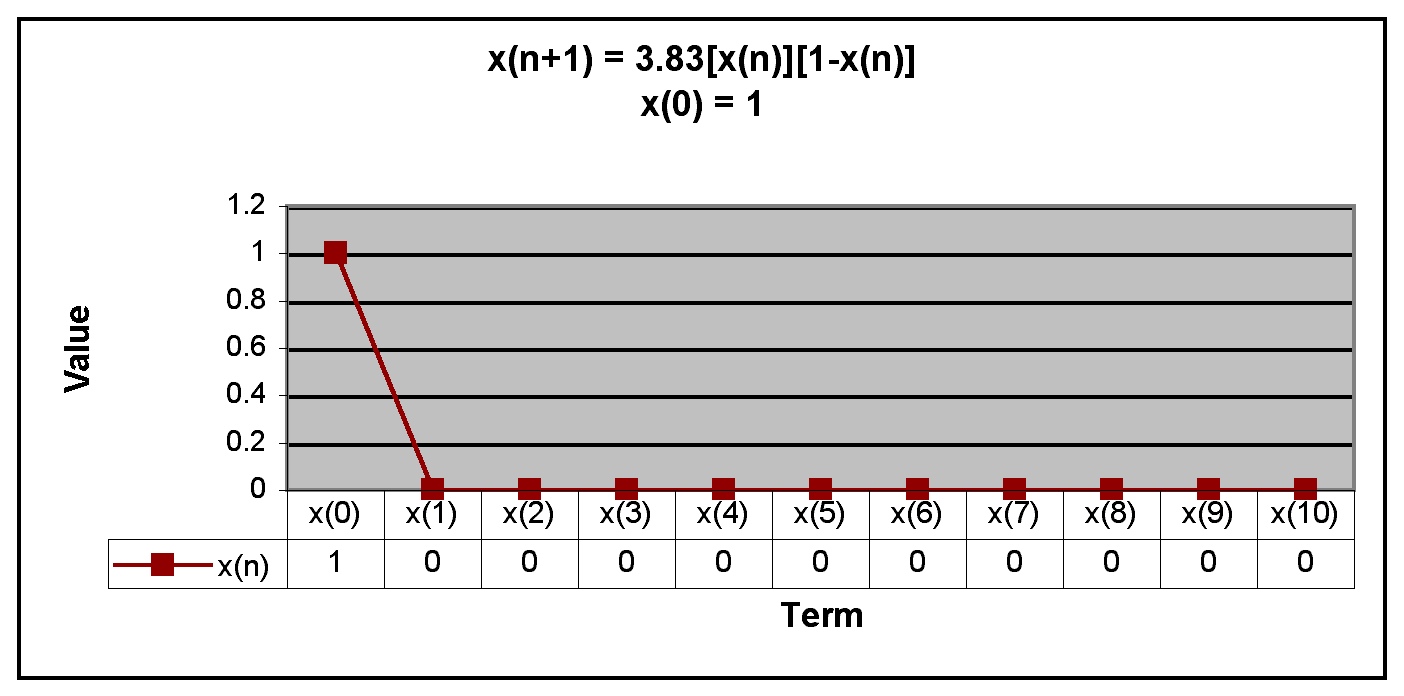
We can see from the graphs that all x(n) are equal to 0 when x(0) is 0 and that all x(n) except x(0) are equal to 0 when x(0) is 1.
Next, we examine when x(0) is equal to a number greater than 1.
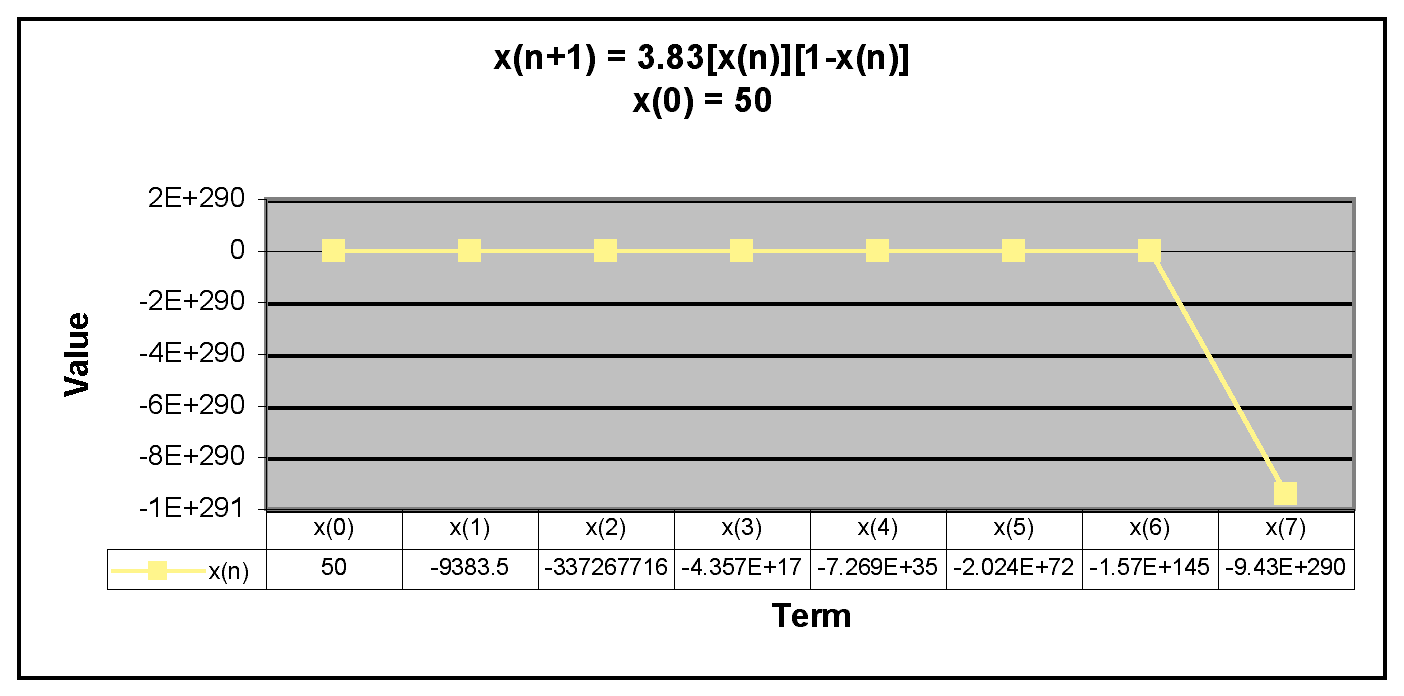
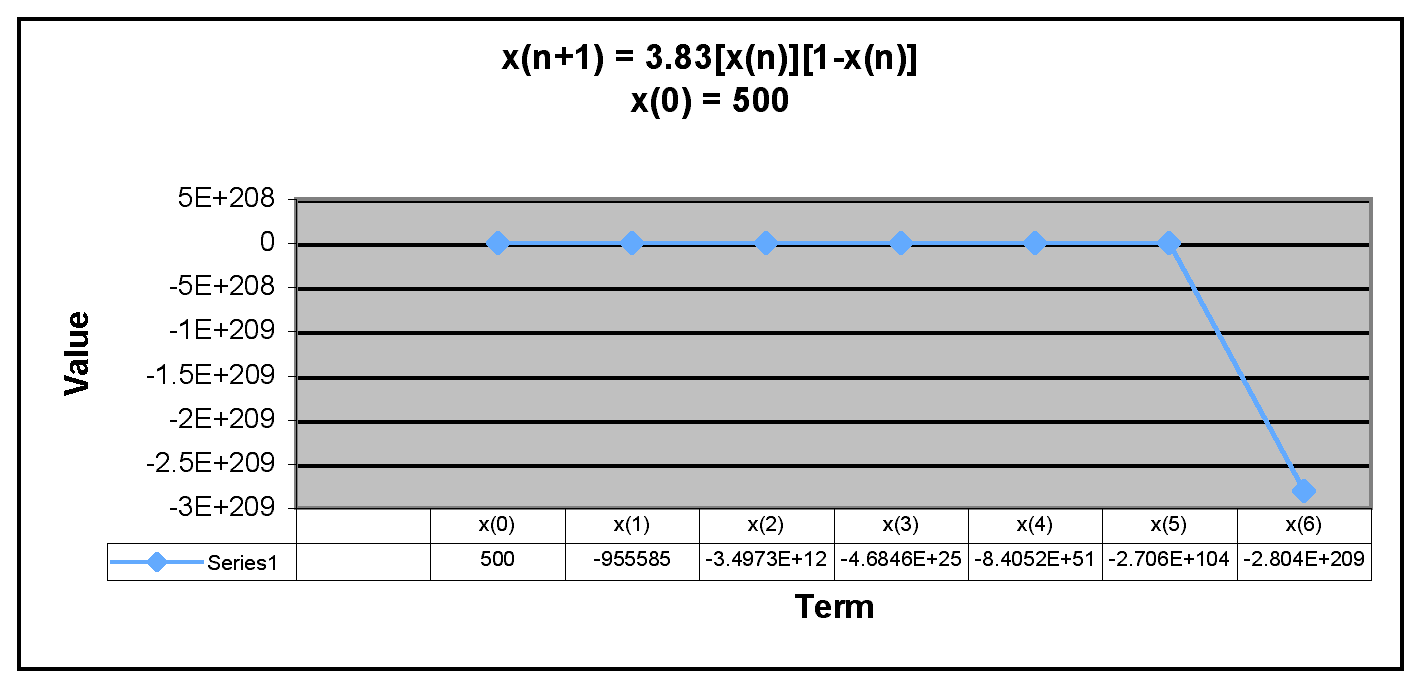
We can see from the graphs that x(n) decreases rapidly when x(0) is greater than 1. This was the case for all x(0) values greater than 1. This is similar to the behavior of the sequence x(n+1) = 3.2[x(n)][1-x(n)].
Next, we examine when x(0) is between 0 and 1.
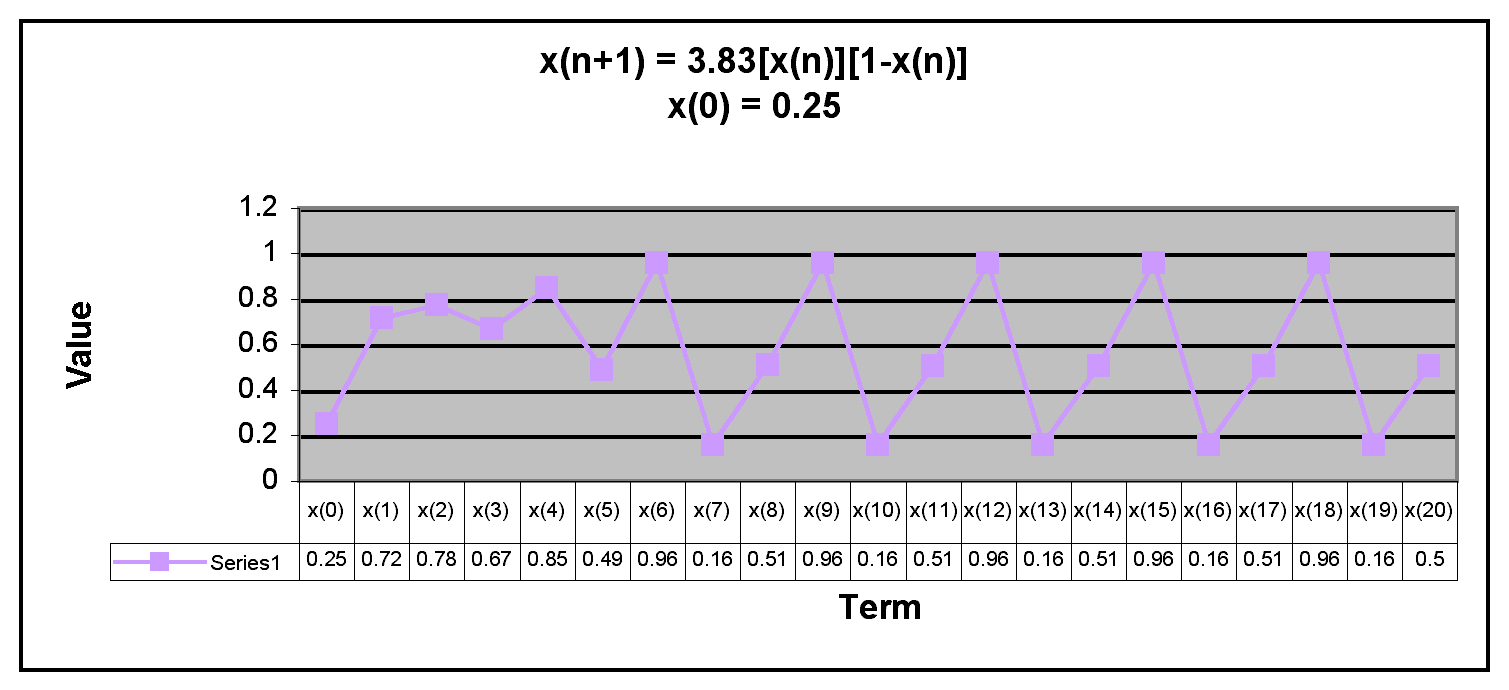
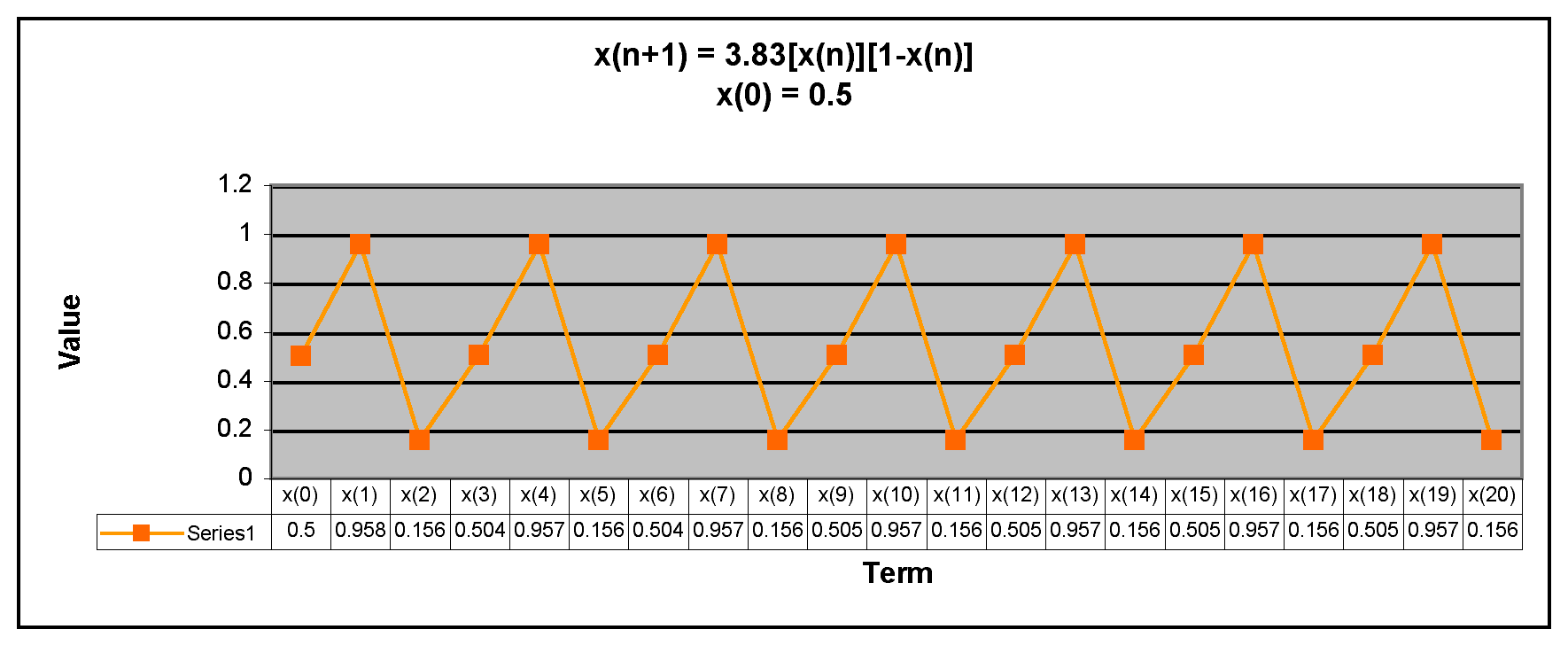
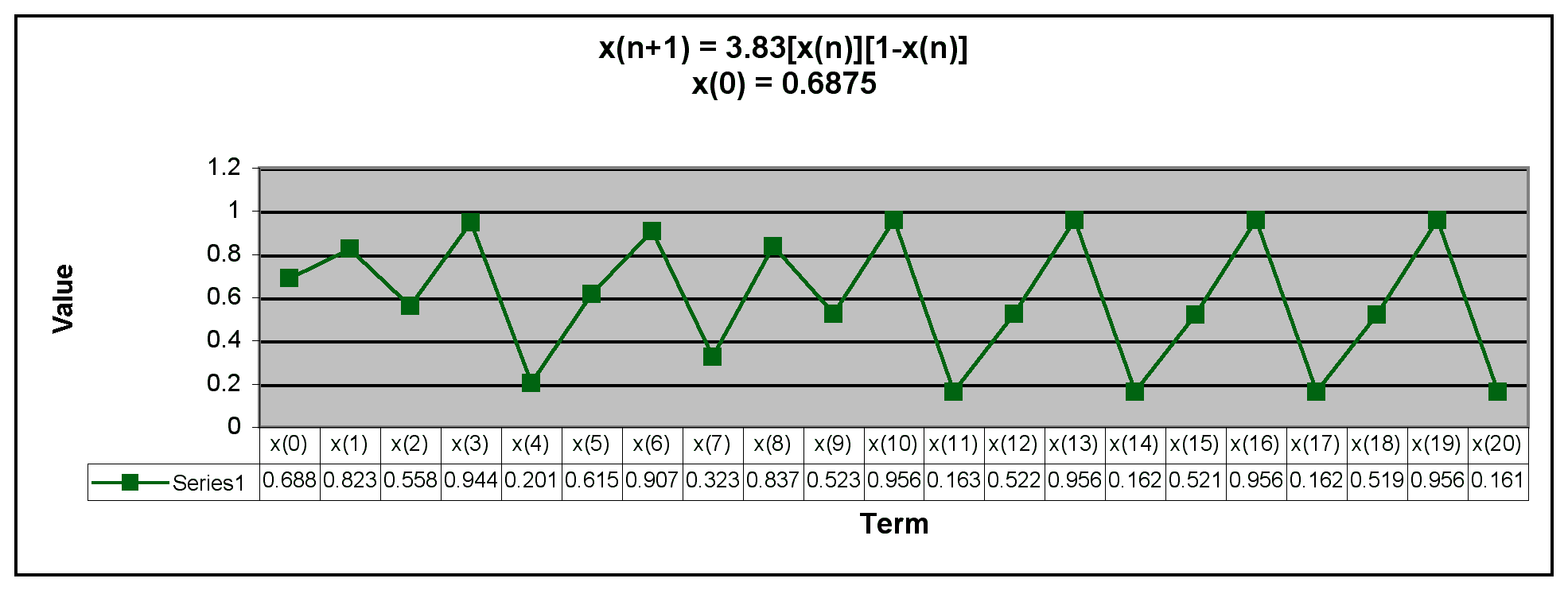
We can see from the graphs that after the first few terms, x(n) appears to develop a pattern when x(0) is between 0 and 1. This is similar to the behavior of the sequence x(n+1) = 3.2[x(n)][1-x(n)].
Next, we will examine negative values of x(0).
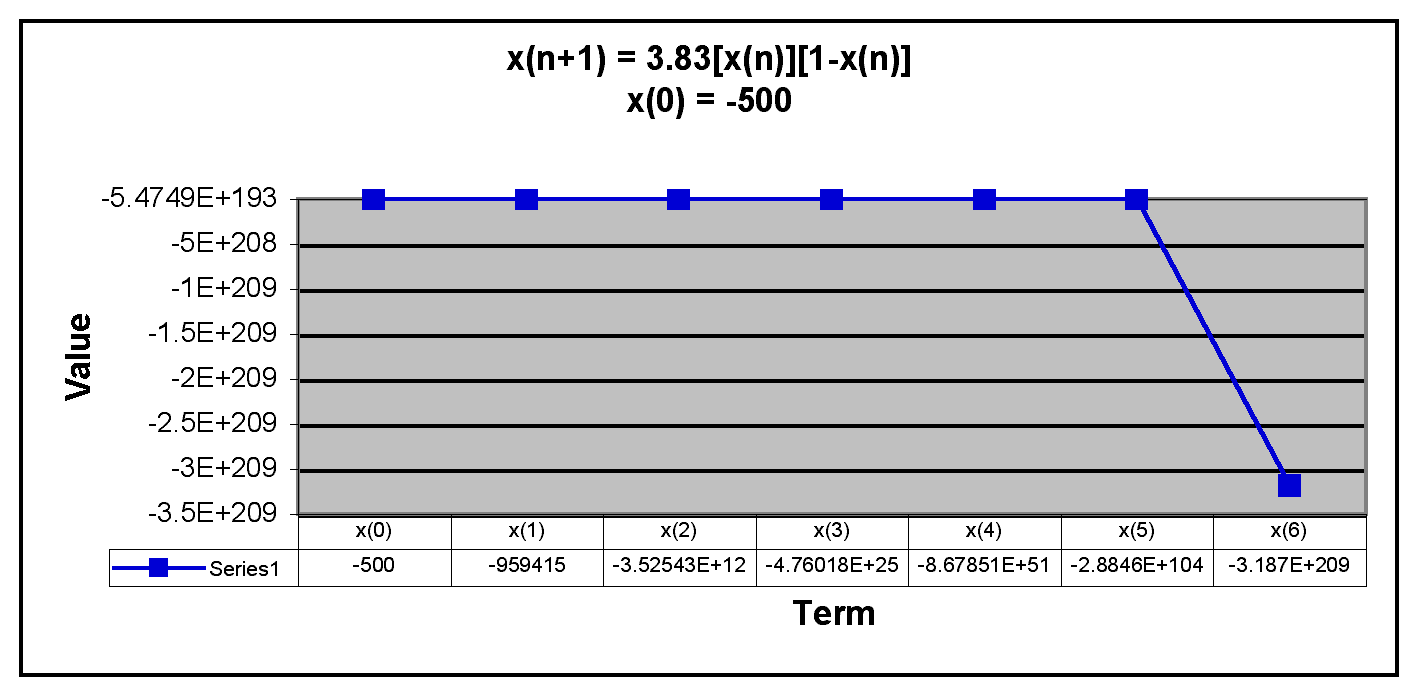
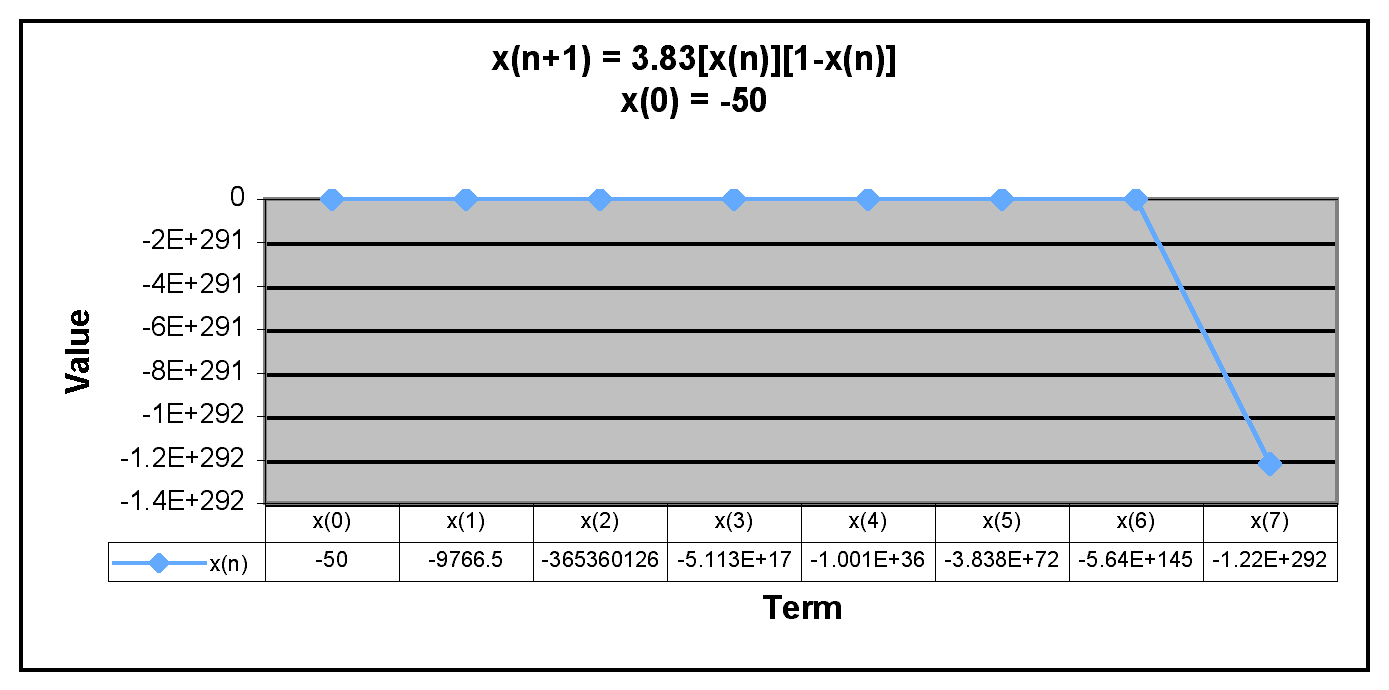
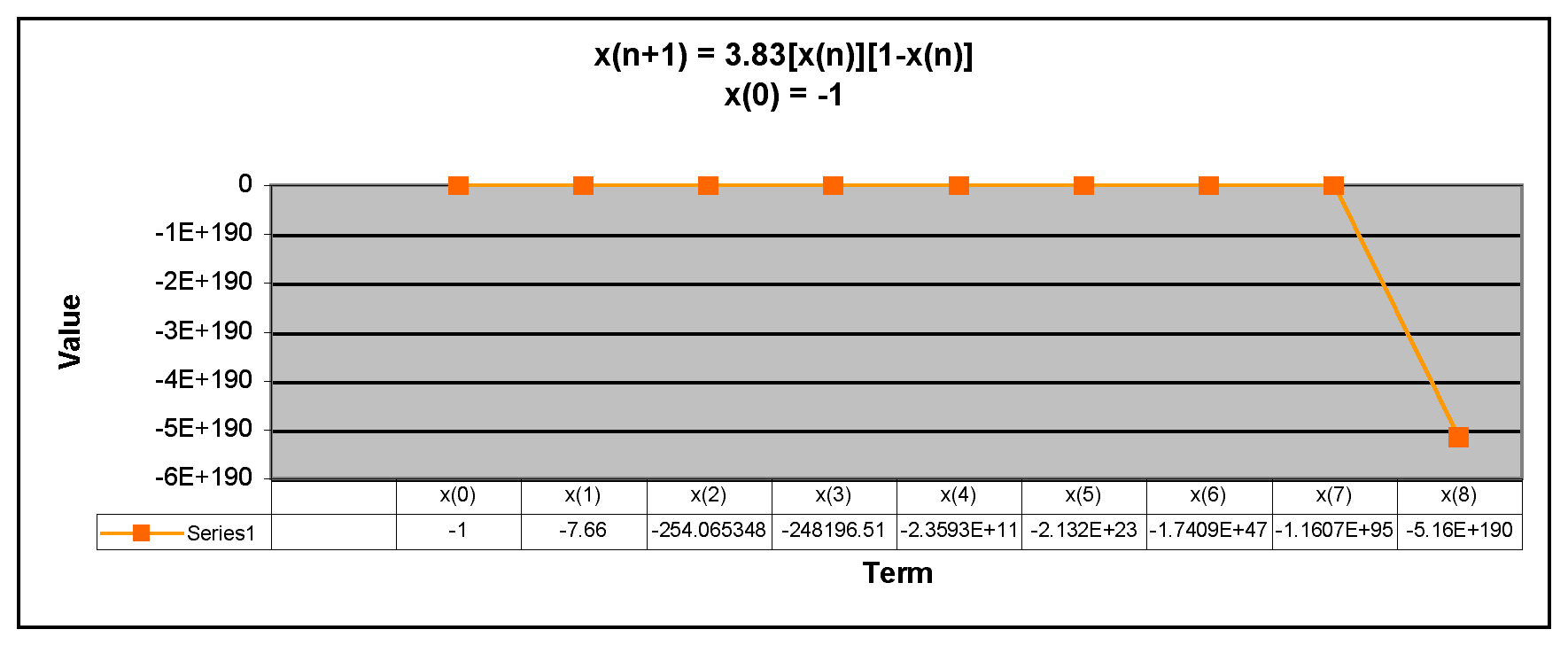
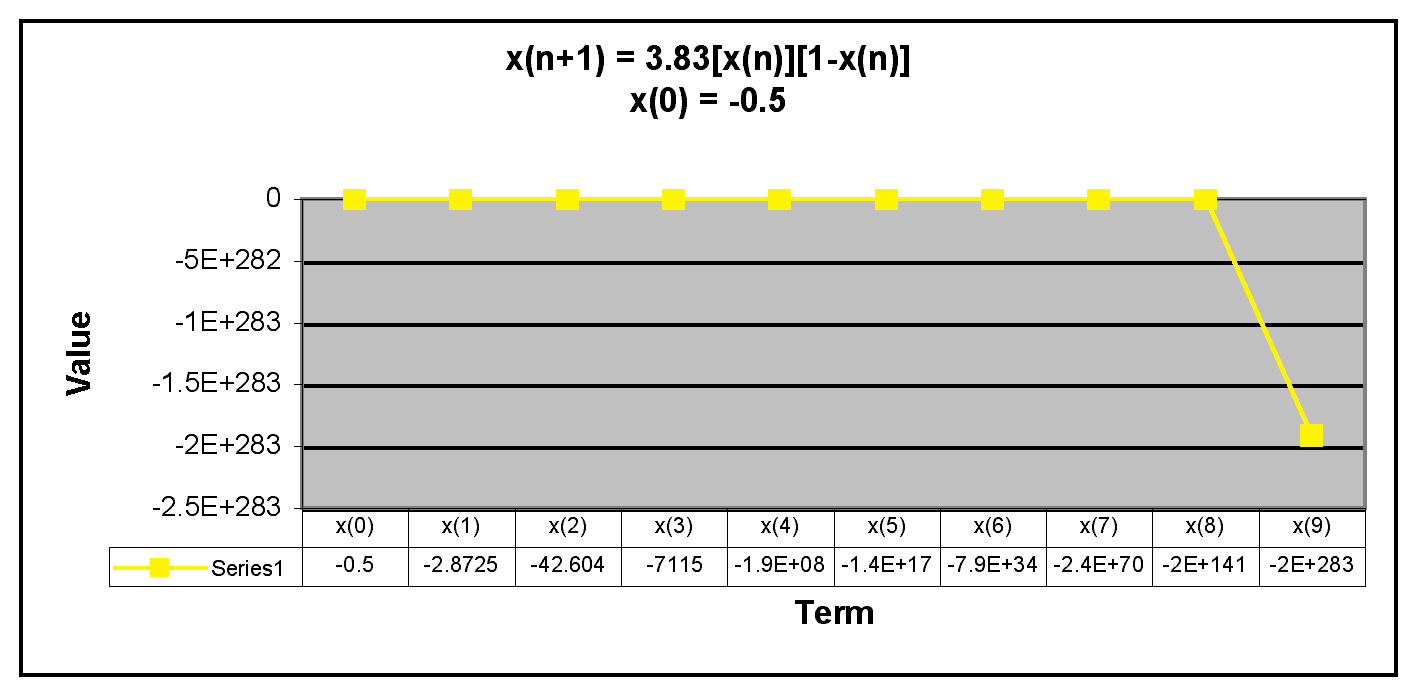
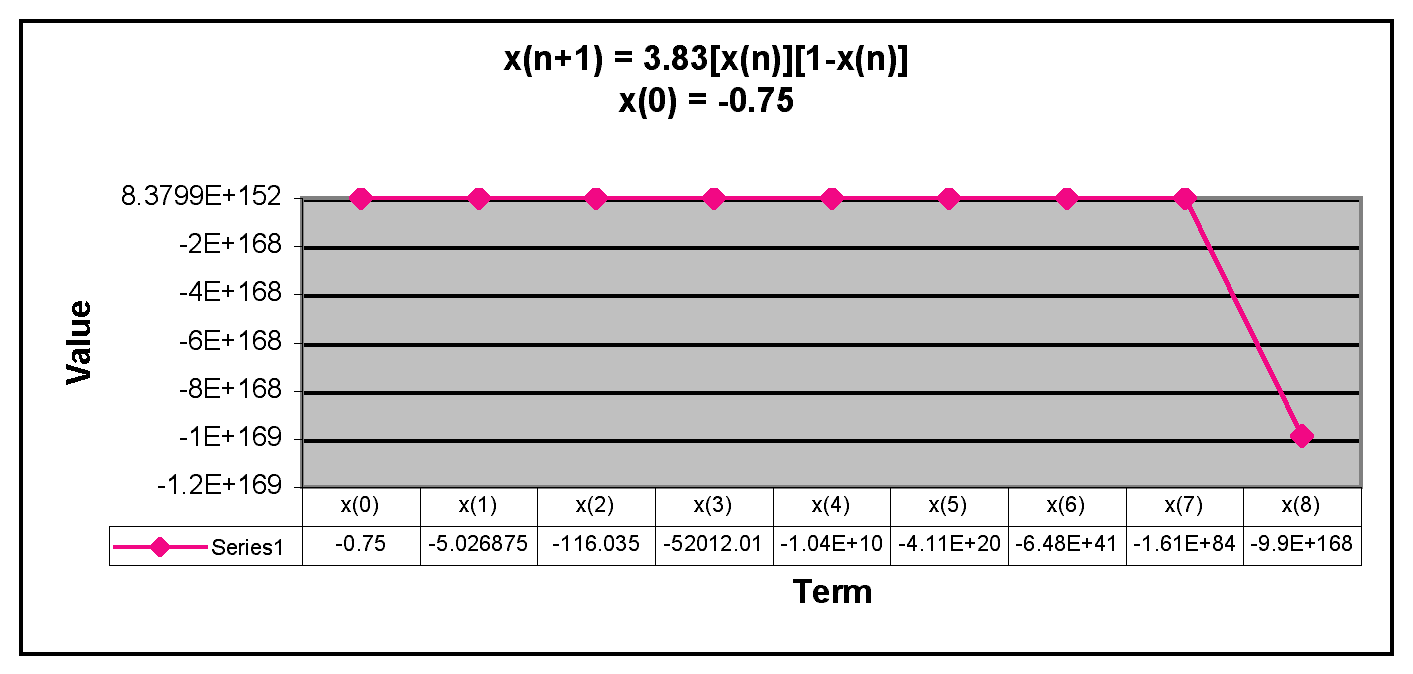
We can see from the graphs that when x(0) is negative, the terms in the sequence decrease rapidly. Thus, the sequence has the same behavior if x(0) is negative or greater than 1. The only time the sequence doesn't descrease rapidly is when x(0) is between 0 and 1. Overall, the behavior of this sequence is very similar to the beahvior of x(n+1) = 3.2[x(n)][1-x(n)].