

Essay 1
Exploring Sequences
Part 3
By
Mandy Stein
Problem 3.
For 0 < A < 2 examine
![]()
for -1 < x(0) < 1
First, we examine the sequence when a = 0.1.
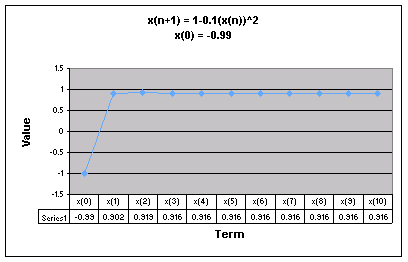
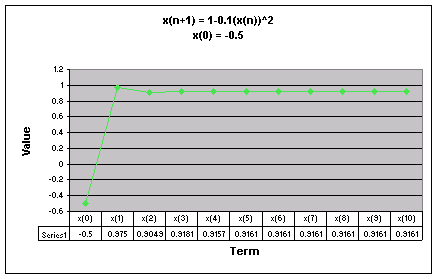
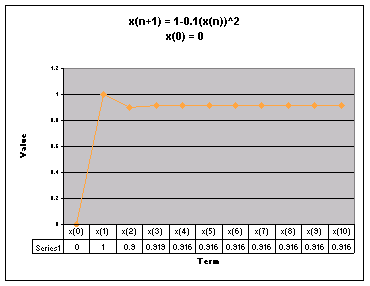
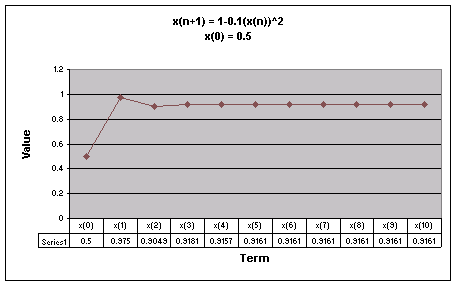
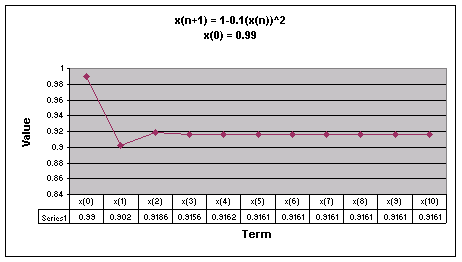
We notice that for all values of x(0) the sequence appears to level out to one number. For all values of x(0) except 0.99 and -0.99, the sequence goes up then back down before it starts to level off.
Let's look at a graph of all of these values of x(0) together when a = 0.1.
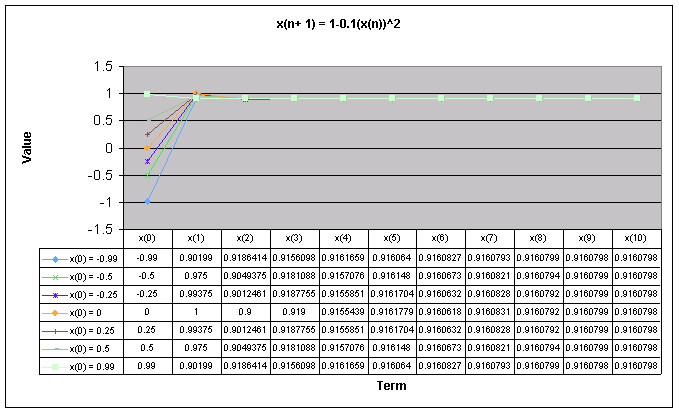
Looking at this graph it is more obvious that regardless of the value of x(0), when a = 0.1 the sequence levels off to 0.9160798.
Next, lets examine the sequence when a = 0.5
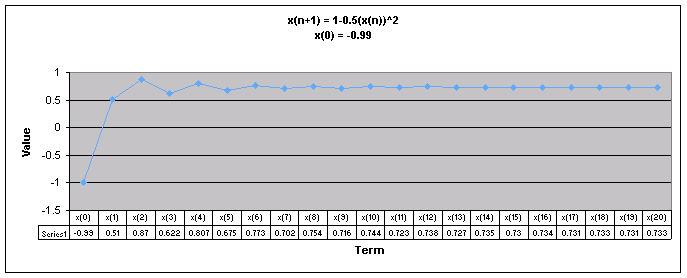
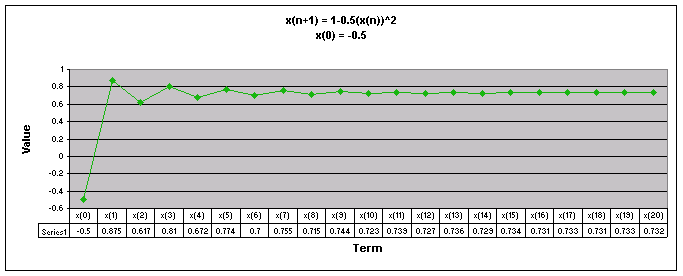
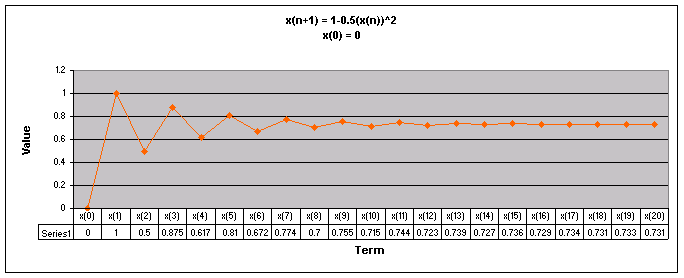
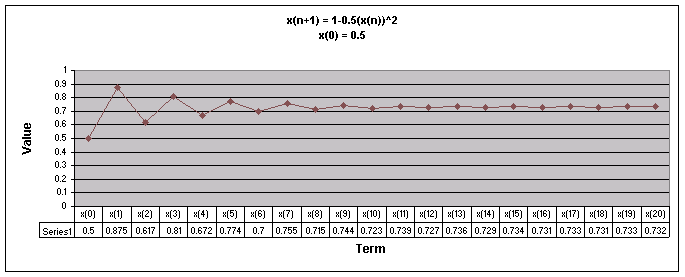
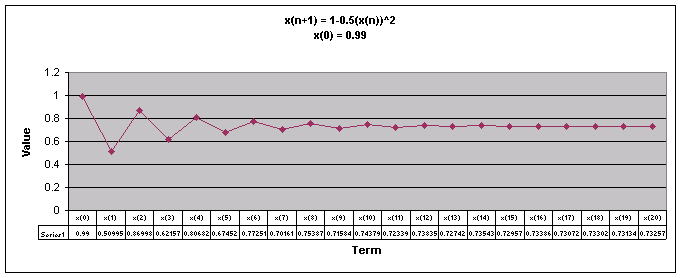
We notice that for all values of x(0) the sequence appears to level out to one number. For all values of x(0) except 0.99, the sequence goes up and down then begins to level off.
Let's look at a graph of all of these values of x(0) together when a = 0.5.

Looking at this graph it is more obvious that regardless of the value of x(0), when a = 0.5 the sequence levels off to 0.732.
Next, lets examine the sequence when a = 0.75
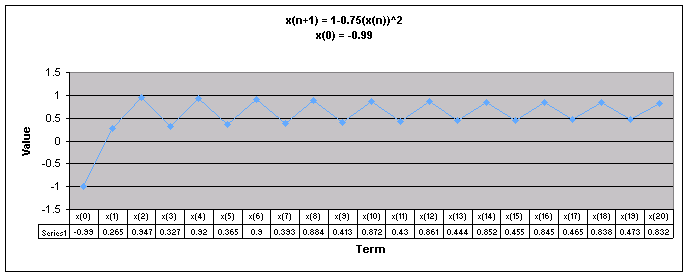
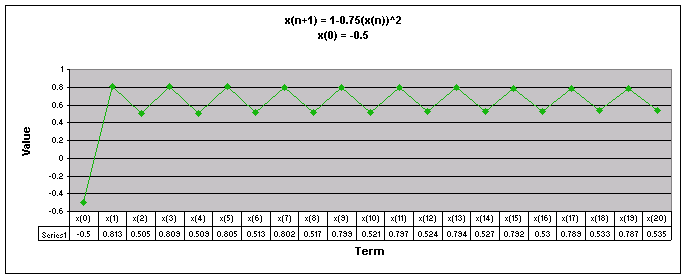
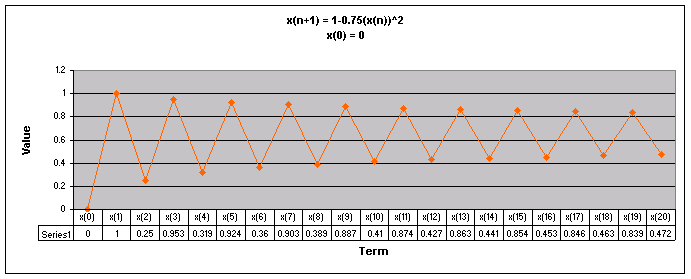
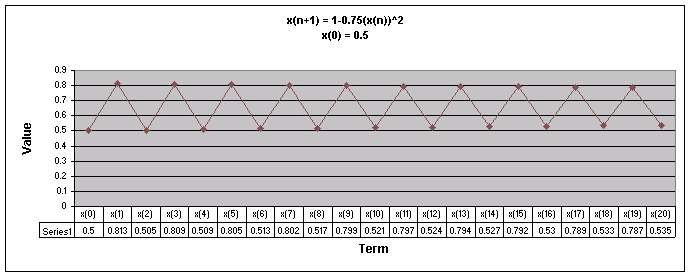
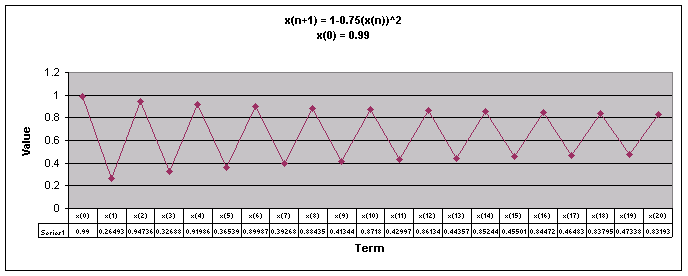
We notice that for all values of x(0) the sequence appears to move up and down eventually oscillating between two numbers.
Let's look at a graph of all of these values of x(0) together when a = 0.75.
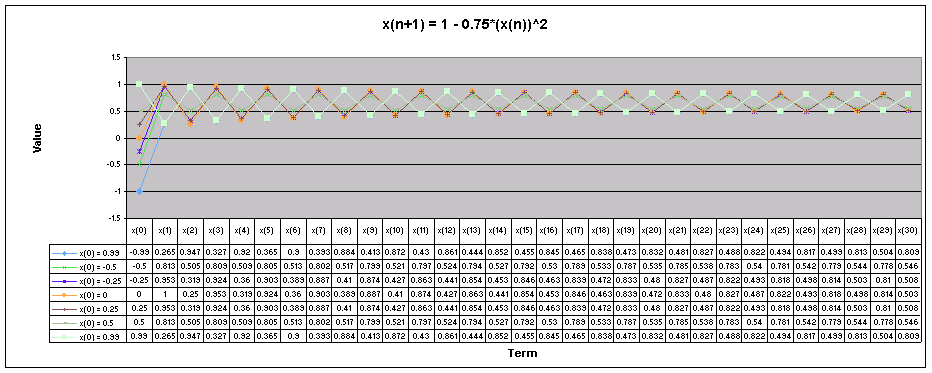
Looking at this graph it is more obvious that regardless of the value of x(0), the sequence oscillates between the same two numbers, the oscillation pattern is just flipped depending on the value of x(0).
Next, lets examine the sequence when a = 1
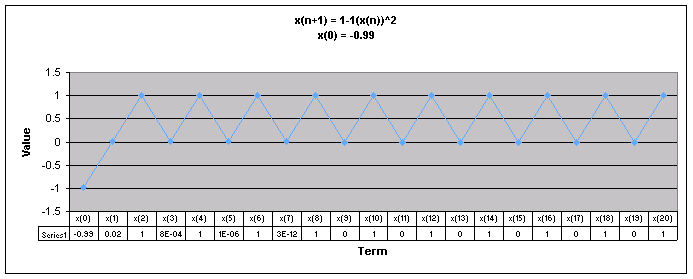
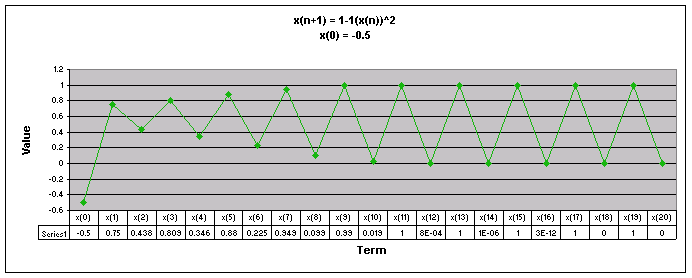
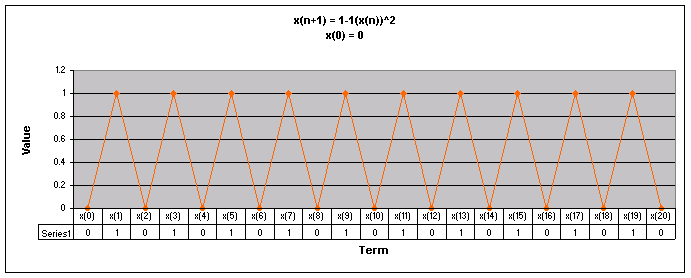
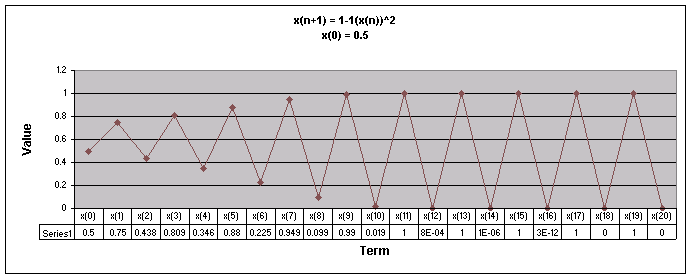
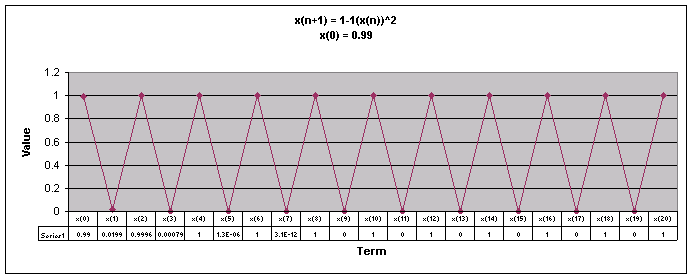
We notice that for all values of x(0) the sequence appears to move up and down eventually oscillating between two numbers.
Let's look at a graph of all of these values of x(0) together when a = 1.
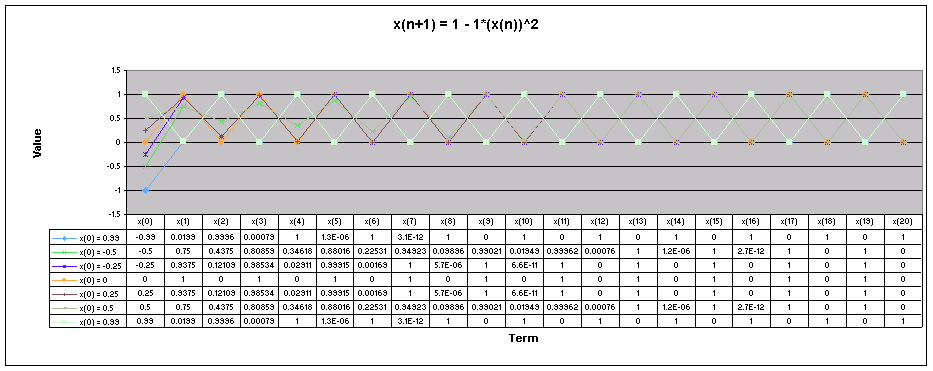
Looking at this graph it is more obvious that regardless of the value of x(0), the sequence oscillates between the same two numbers, the oscillation pattern is just flipped depending on the value of x(0).
Next, lets examine the sequence when a = 1.5.
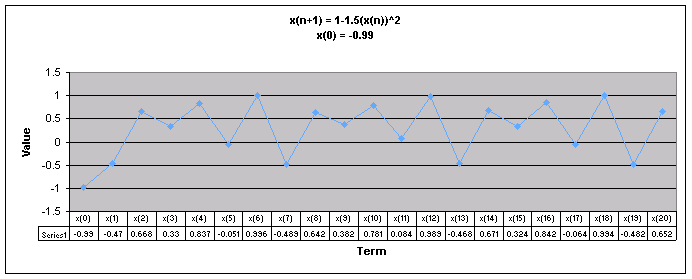
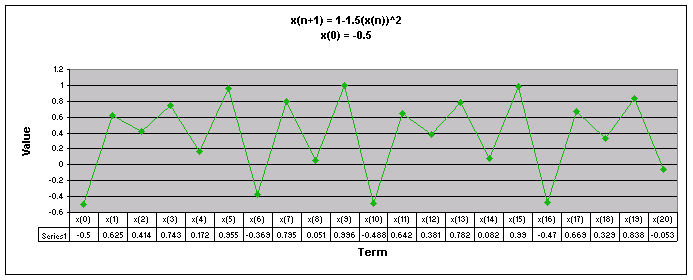
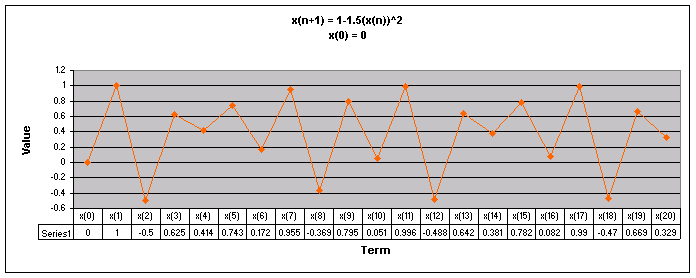
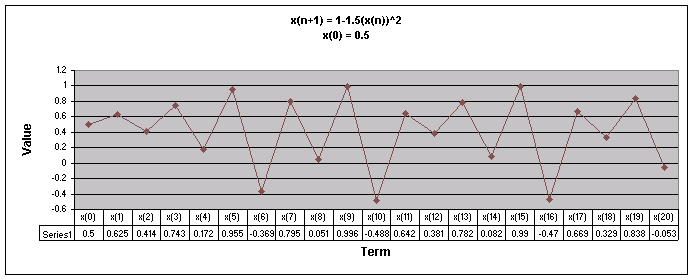
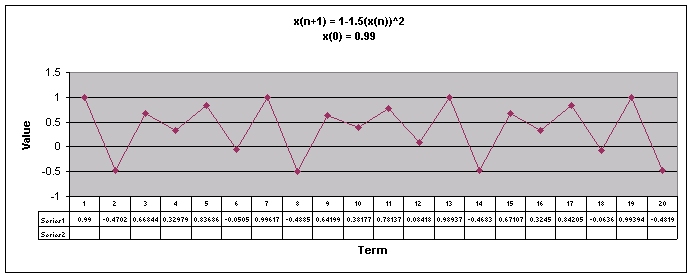
We notice that for all values of x(0) the sequence appears to follow a repeating pattern moving up and down.
Let's look at a graph of all of these values of x(0) together when a = 1.5
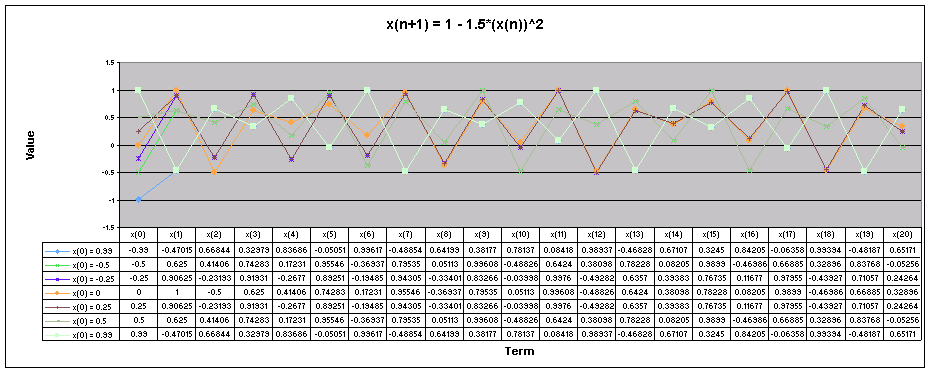 .
.
Looking at this graph we can see that even though the sequence follows a repeating pattern, the patterns do not coincide to the same numbers as with the other values of a.
Next, lets examine the sequence when a = 1.99.
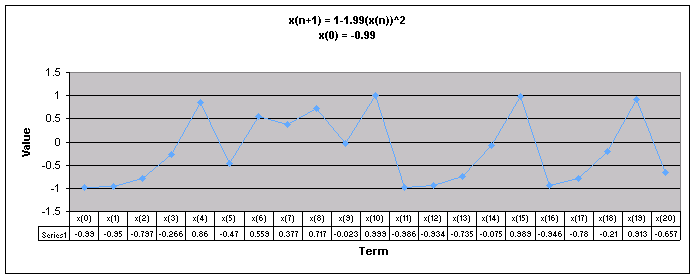
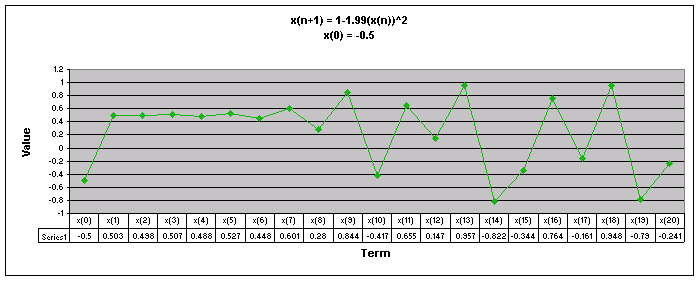
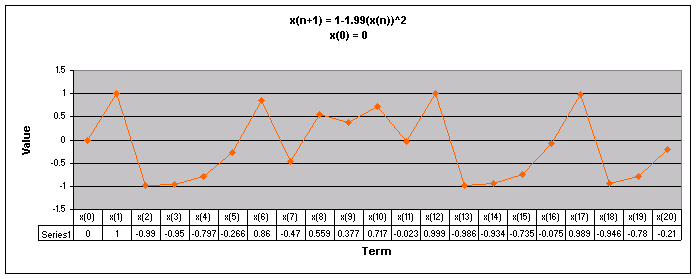
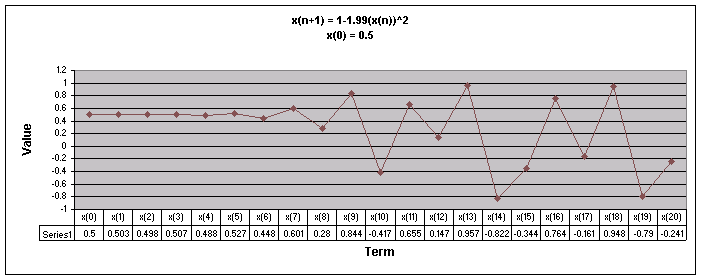
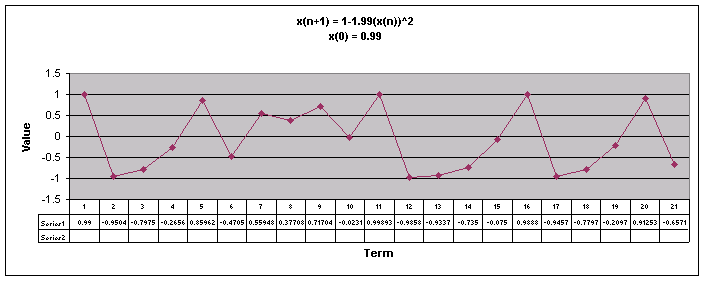
We notice that for all values of x(0) the sequence appears to follow a repeating pattern moving up and down.
Let's look at a graph of all of these values of x(0) together when a = 1.99.
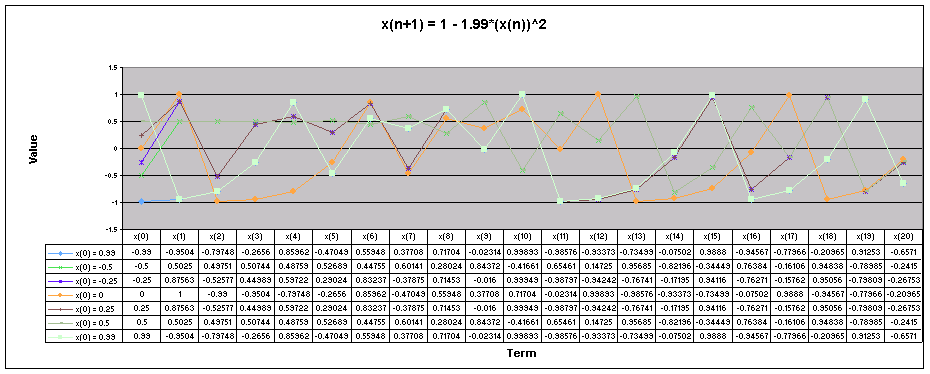
Looking at this graph we see that the sequence follows different paths depending on the value of x(0). The sequence appears to fall into a repeating pattern as the sequence progresses.