

Conics Instructional Unit
Day 9 - Parametric and Polar Equations
by
Mandy Stein
Parametric Equations
Circles and Ellipses
A parametric curve in the plane is a pair of functions, called the parametric equations of a curve,
x = f(t)
y = g(t)
where the two continuous functions define ordered pairs (x, y). The extent of the curve will depend on the range of t.
A circle and an ellipse can be graphed using the parametric equations
x = a cos (t)
y = b sin (t)
0 < t < 2p
If |a| is equal to |b|, the graph produces a circle with center (0,0) and a radius equal to |a|. If |a| and |b| are different, the graph produces an ellipse with a horizontal axis of 2|a| and a vertical axis of 2|b|.
Let's look at some graphs to illustrate this concept.
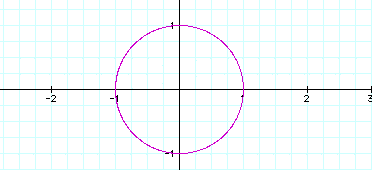
x = cos (t)
y = sin (t)
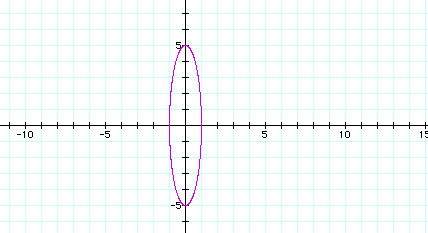
x = cos (t)
y = -5 sin (t)
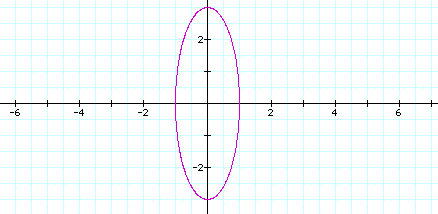
x = cos (t)
y = 3 sin(t)
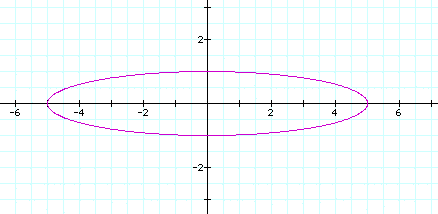
x = -5 cos (t)
y = sin (t)
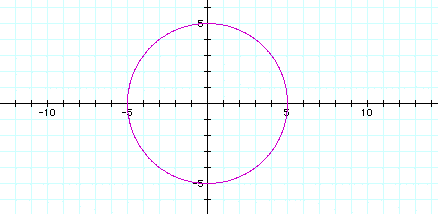
x = 5 cos (t)
y = 5 sin (t)
Polar Equations
Parabolas and Hyperbolas
A parabola and a hyperbola can be graphed using the polar equations
![]()
![]()
![]()
![]()
The first equation we will examine is
![]()
When k = 1, this equation produces a variety of parabolas, opening left when p is negative and right when p is positive.
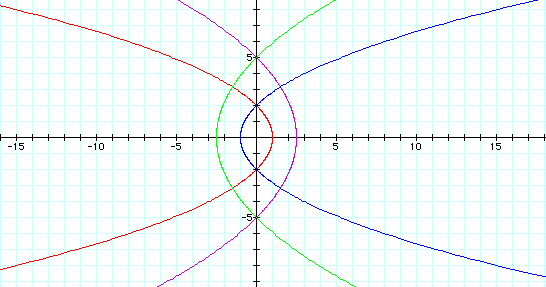
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is greater than 1, the equation produces a hyperbola with a horizontal transverse axis and the asymptotes of the hyperbola.
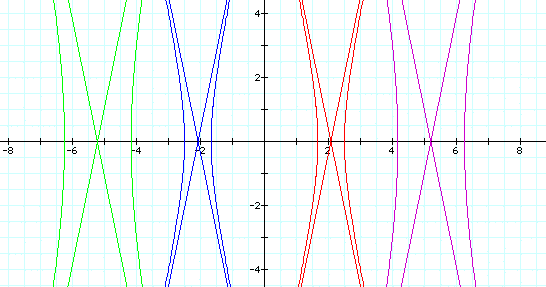
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is less than 1, the equation also produces a hyperbola with a horizontal transverse axis and the asymptotes of the hyperbola.
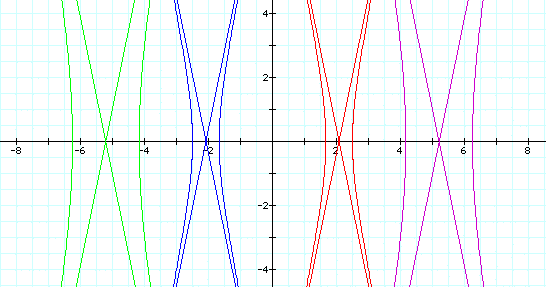
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
Next, we examine
![]()
When k = 1, this equation produces a variety of parabolas, opening left when p is positive and right when p is negative.
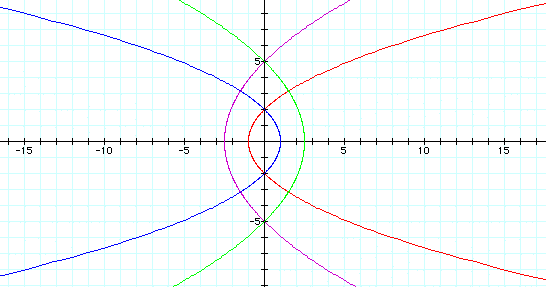
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is greater than 1, the equation produces a hyperbola with a horizontal transverse axis and the asymptotes of the hyperbola.
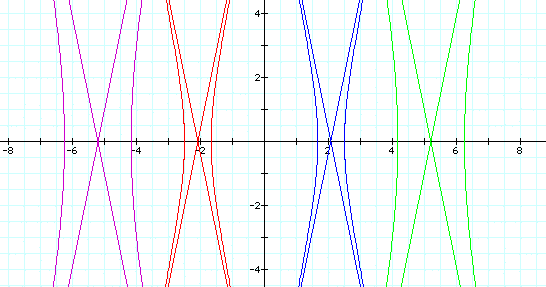
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is less than 1, the equation also produces a hyperbola with a horizontal transverse axis and the asymptotes of the hyperbola.
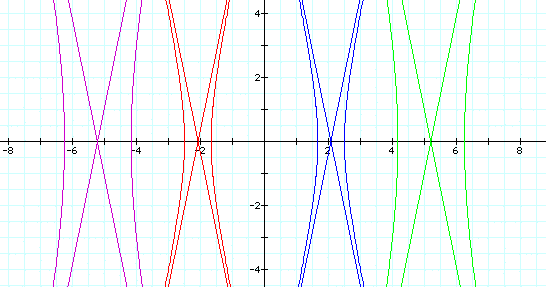
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
Next, we will examine the graph of
![]()
When k = 1, this equation produces a variety of parabolas, opening up when p is positive and down when p is negative.
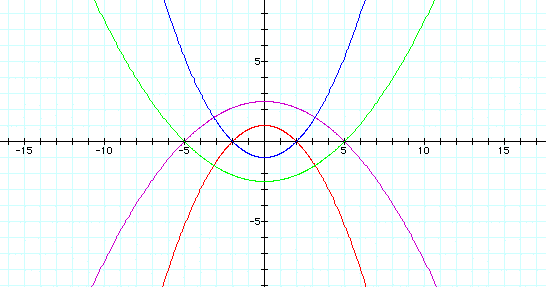
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is greater than 1, the equation produces a hyperbola with a vertical
transverse axis and the asymptotes of the hyperbola.
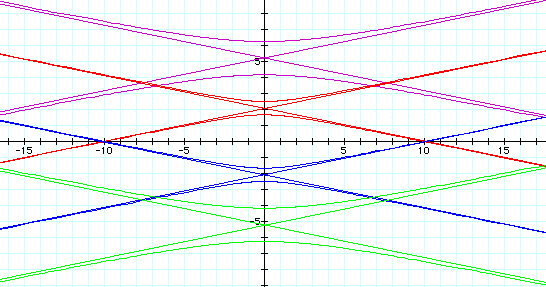
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is less than 1, the equation also produces a hyperbola with a vertical transverse axis and the asymptotes of the hyperbola.
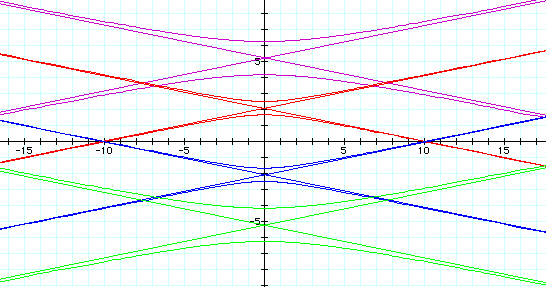
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
Next, we will examine the graph of
![]()
When k = 1, this equation produces a variety of parabolas, opening down when p is positive and up when p is negative.
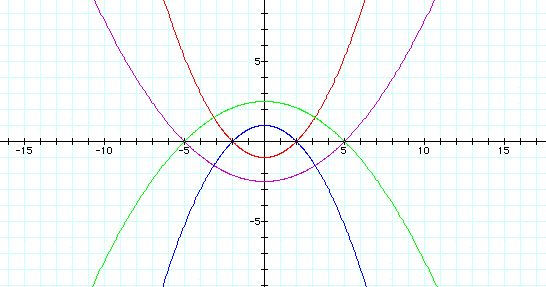
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is greater than 1, the equation produces a hyperbola with a vertical
transverse axis and the asymptotes of the hyperbola.
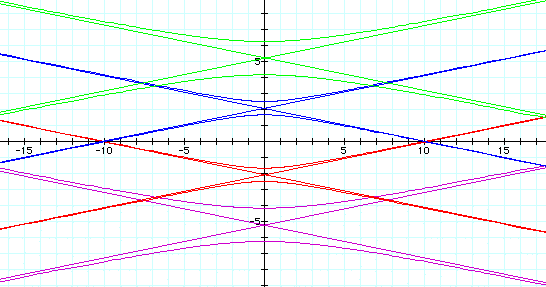
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph
When k is less than 1, the equation also produces a hyperbola with a vertical transverse axis and the asymptotes of the hyperbola.
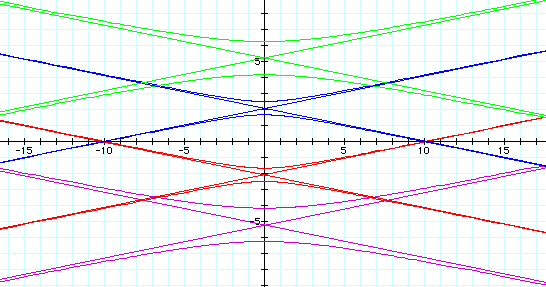
p = -5 is the purple graph
p = -2 is the red graph
p = 2 is the blue graph
p = 5 is the green graph