Square Within a Square
Nicole Mosteller
EMAT 6690
What happens to
the area of square WXYZ as
point 1 moves out
side of square ABCD?
Adaptations to be Made
To investigate the idea of point 1 moving out
of the original square, a few adjustments needed to be made to
the construction of our square. The original square was constructed
onto a coordinate plane with the sides of the square extended
to be lines. The sides of the inside square were reconstructed
as well so that instead of segments, the sides are lines. The
reconstruction does not effect the original property of the squares,
but allows for further manipulation.
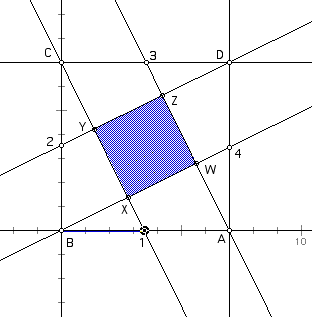 Graph 1: Squares on Coordinate Plane
Graph 1: Squares on Coordinate Plane
To answer the original question, let's
manipulate point 1 along line BA.
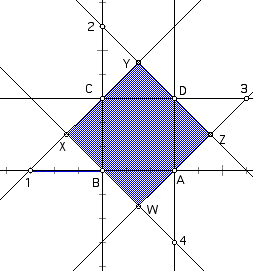 Graph 2: As point 1 moves in the negative
direction from square ABCD, notice that square WXYZ grows larger.
Infact while viewing the animation of point 1 along line AB (in
the negative direction), square WXYZ seems to grows a maximum
of twice as large as square ABCD. After reaching this peak, square
WXYZ subsides and approaches the same area as square ABCD (See
Graph 4).
Graph 2: As point 1 moves in the negative
direction from square ABCD, notice that square WXYZ grows larger.
Infact while viewing the animation of point 1 along line AB (in
the negative direction), square WXYZ seems to grows a maximum
of twice as large as square ABCD. After reaching this peak, square
WXYZ subsides and approaches the same area as square ABCD (See
Graph 4).
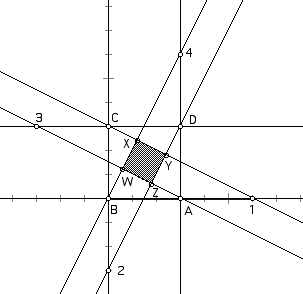 Graph 3: As point one moves in the
positive direction from square ABCD, notice that the square WXYZ
continues to grow in area. While viewing the animation of point
1 along line AB (in the positive direction), square WXYZ's area
continues to approach the area of the original square ABCD (See
Graph 4).
Graph 3: As point one moves in the
positive direction from square ABCD, notice that the square WXYZ
continues to grow in area. While viewing the animation of point
1 along line AB (in the positive direction), square WXYZ's area
continues to approach the area of the original square ABCD (See
Graph 4).
In order to see exactly how the area
of square WXYZ changes in respect to the area of square ABCD as
point 1 moves along line AB, below is a graph of the trace of
a point that shows the relationship.
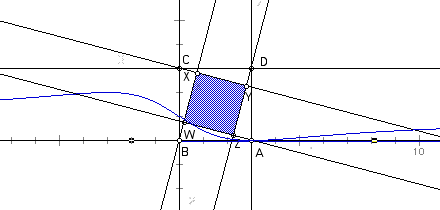 Graph 4: After tracing a point that
shows the relationship where
x = position of point 1 in respect
to point B
y = the ratio of areas of squares WXYZ:ABCD,
our square problem has evolve from
just a geometrical investigation of two squares to finding an
algebraic representation of the relationship (x, y).
Graph 4: After tracing a point that
shows the relationship where
x = position of point 1 in respect
to point B
y = the ratio of areas of squares WXYZ:ABCD,
our square problem has evolve from
just a geometrical investigation of two squares to finding an
algebraic representation of the relationship (x, y).
How do we find the
equation for the line created by the traced point (x, y)?
Return
to Intro to Square | Previous
Page | Further Investigation




