Square Within a Square
Nicole Mosteller
EMAT 6690
How do we find the
equation for the line created by the traced point (x, y)?
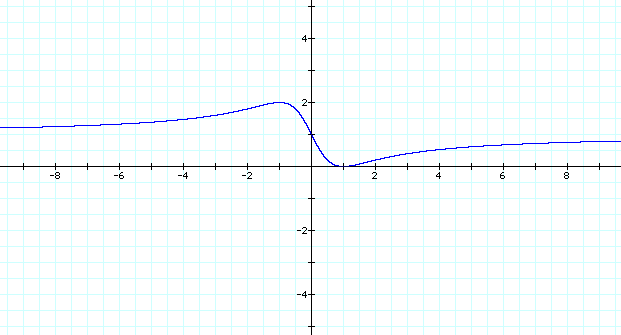Graph 1: Recall from the previous investigation,
the line above represents the trace of the point (x, y) where
x = the position of Point 1 as it animates
along line AB, and
y = the ratio of the area of the squares
WXYZ:ABCD.
Method of Investigation
Although other
investigations into this problem have used the distance
formula to arrive at an equation for the graph of the above line,
I have chosen to use several of the known values in the graph
and approach an eqation for the graph using calculus.
Given Information
from the Graph
There are several known values from
the graph: (-1, 2), (0, 1), and (1,0).
A maximum value occurs at x = -1, and
a minimum value occurs at x = 1.
There is a horizontal asymptote at
y = 1.
An inflection point is at (0,1).
Additional known
Facts
From the given information and from
the nature of the graph, we can assume several additional facts
about the equation of the curve.
* The horizontal asymptote symbolizes
a rational equation (polynomial divided by a polynomial).
* Because the asymptote occurs at y
= 1, the polynomials must be of the same degree, and their lead
coefficients must be equal.
* Polynomials of odd degrees can be
ruled out because of the number of roots.
The Equation
Using the given information and additional
know facts, let's start our investigation using an equation of
degree two.
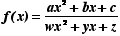
Return
to Intro to Square | Previous
Page | Further Investigation