

Problem: 100 degree Isosceles Triangle
Given an isoscles triangle
ABC with AB = AC and the measure of angle BAC = 100 degrees. Extend
AB to point D such that AD = BC. Now
draw segment CD. What is the size of angle BCD?
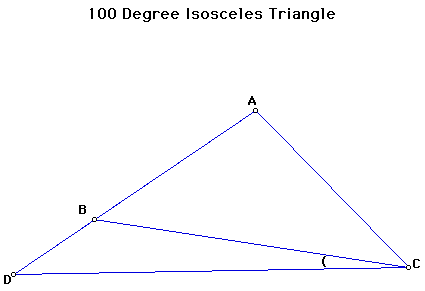
Note: There can be several different approaches to this problem. Geometric arguments are preferred to using trigonometry.
Ususally, a solution to a problem
such as this requires some auxilliary constructions.
Do you want a Hint for one auxillary construction?
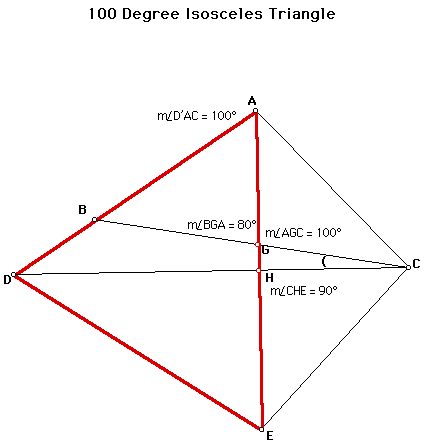
First, I created the lines of reflection in CD with DE and CE constructed. I constructed point E with the two segments reflected about segments AD and AC.
Second, with D as the center and segment AD as the radius, I constructed arc 1, using E as the center and segment AE as the radius, I constructed arc 2 and I drew AE and DE.
Since we used radius AD as a guide then AD = DE = AE. Thus, triangle ADE is an equilateral triangle.
Therefore, <AGC = 100 degrees because <EAC = 40 degrees and <ACD = 40 degrees, by angles in a triangle measuring 180 degrees.
Because <AGC = 100 degrees, <AGB = 80 degrees by supplementary angles. And <CGE = 80 degrees by opposite angles, just as <BGE = 100 degrees.
Look at segment DC, it is the angle bisector of <ADE, therefore, segment AE is a perpendicular bisector of this angle creating 90 degree angles.
Now, I have <CGE = 80 degrees and <CHE = 90 degrees. And by definition of a triangle being a total of 180 degrees, then <BCD = 10 degrees.
Find alternative solultions or compre your solution to the solutions of others to see alternative approaches.
Click here to see the solution of the 100 degree Isosceles Triangle: