Calculus

by: Kelli Nipper

The quantity to be maximized - the dependent variable- is the volume V of the box to be constructed. The shape and thus the volume of the box are determined by the length x of the edge of each corner square removed. Hence, X is the independent variable.

To write the volume V as a function of X, we note that the base will measure (15 - 2x) inches by (25 - 2x) inches and the height is x giving:

Procedure for finding the absolute extrema of a continuous function f on [a,b]:

Step 1: Find the quantity to be maximized:

Step 2: Express the dependent variable as a function of the independant variable:

Step 3: Apply Calculus to find the critical points:

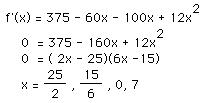
Step 4: Identify the extrema:

x= 0 , 7.5

Step 5: Answer the question posed in the problem:

Question : The maximum volume of the box occurs when x (the height) = 3.9. This yields a volume of : 482.976 cubic inches

Return to Maximizing Volume Page