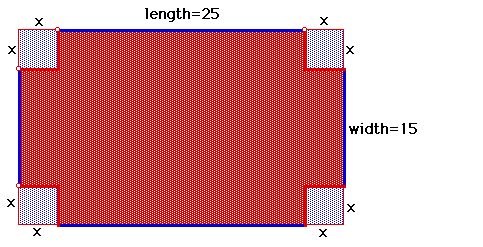
In order to use any program, first students will need to understand the question and be able to determine the corresponding equation. Using the diagram, the length is (25 - 2x) the width is (15 - 2x) and the height is x. Since Volume = Length * Width * Height, V(x) = (25 - x) (15 - 2x) (x).

Beginning with a demonstration using The Geometer's Sketchpad helps to visualize the question at hand. It naturally sets up the stage for connecting the geometrical perspective to algebra using The Algebra Xpresser. After the explorations with variables. The Excel spreadsheet can be used by inputting values into the function. These three software programs help to connect geometrical, algebraical, and functional approaches in one exploration. The results from these estimates can be used to introduce and support the Calculus of finding the maximum value.