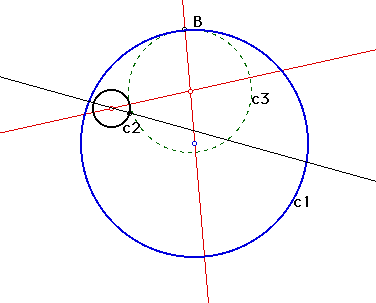

The last conjecture focused on the connections between the centers of c2 and c3. If we are able to observe any relationships between these circles, we should be able to begin to understand how to construct the tangent circle given only the original circle c1 and the internal circle c2.
Looking only at the line connecting the centers and the line from point B to the center of c1 it is difficult to see a connection between them. They do not seem to be perpendicular. They certainly are not parallel. Is there any special connection?
As trite as it may seem, the fact they intersect is very important.
Look at the distance from the center of circle c2 to the intersecting line. Can you define the distance?
Click Here to continue the investigation.