Click here for the original question.
The formula for the volume of a cone is
![]() .
.
The circular disk has a circumference of 2 (pi) r. The arc of the circle that is removed from the disk is x = theta*r / (2*pi) where r = R (1 - theta / 2 pi).
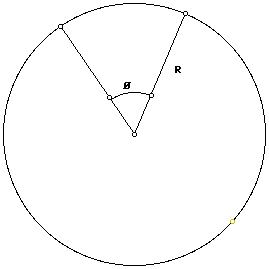
By Pythagorean Theorem, h = sqrt(R^2 - r^2) = sqrt(R^2 - R^2 (1 - theta / 2 pi)^2).
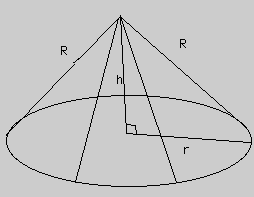
At this point we have two (h and r) of the three variables in terms of R (a constant) and theta. Thus, we can substitute and graph to find the maximum volume.
![]()
![]()
On a TI-85 calculator I graphed the above equation for R = 5 cm. The graph looks as follows:
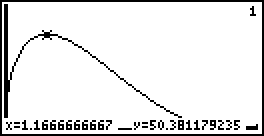
I used the FMAX function to determine the maximum of the function. The result was theta ~ 1.167 radians and V ~ 50.38 cm^3.
I wasn't confident of my above solution. So, I tried another method using a spreadsheet. I have set it up for any value of R.
The second column is the angle phi in tenths, hundredths, or thousandths of pi radians.
The third column is the length of the remaining circumference of the disk [2*pi*R - phi*R].
The fourth column is the diameter of the base of the cone [2r].
The fifth column is the radius, r, of the base of the cone.
The sixth column is the height, h [see formula above], of the cone. The last column is the volume of the cone.
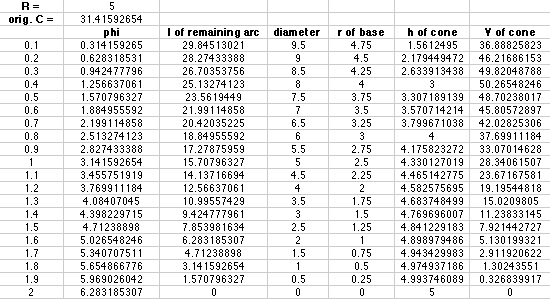
Between 0.3 pi and 0.5 pi, the maximum volume occurs. So I looked at smaller intervals.
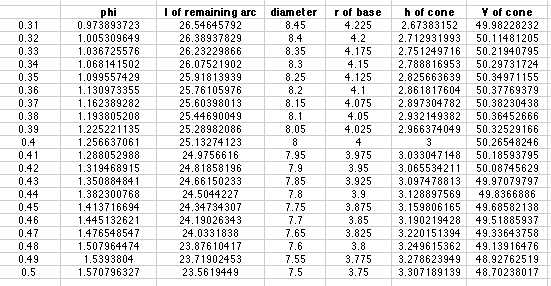
Between 0.36 pi and 0.38 pi, the maximum volume occurs. So I again looked at smaller intervals.
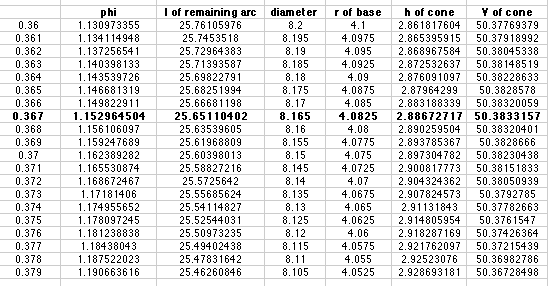
I could keep looking at smaller intervals for better precision. However, I'll estimate the volume as 50.383 cm^3 using an angle of 0.367 pi radians.