What Happens When h = -j?
For studying the case where h and j are different, we need
to fix either h or j and then change the other parameter.
We know for our previous work that for h = -1 we get a vertical line;
nevertheless there are differences when j is positive or negative.
For j positive the length of the line varies, approaching to 0 as j
gets large. And for j negative we got an infinite line.
We know also that for big values of h and j the graph will
be approaching to (0,0).
Let's consider what happens when j = -h.
This first graph was taken with h ranging from 1 to 9:
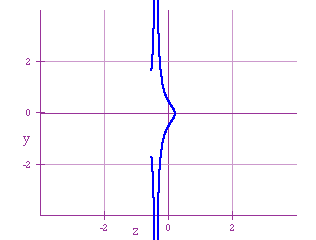
The graph has 2 'arms'; the left one is 'broken' while the right one
is continuous. The gap in the 'broken' arm gets wider for large values of
h. The graph seems to have an asymptote, somewhere between -1 and
0. As h approaches to infinity the gap gets very, very wide; After
9 the length of the right arm of the graph begins to reduce:
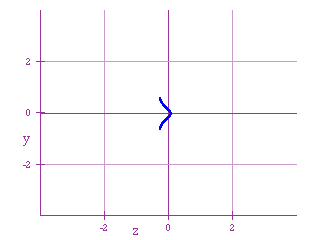
And for large values of h, the graphs goes to zero. This makes sense
from the definition of x and y; since for big values of h the denominators
of both fractions go to zero. The behavior is similar if the roles of h
and j are interchanged.
Back


