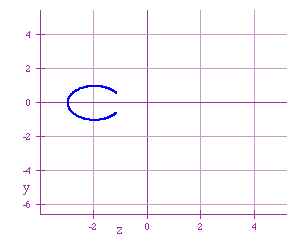

For k > -1, the graph still looks like an inverted C:
The bigger k, the 'longer' the graph! Also the 'arms' of the inverted C
seems to be 'moving', approaching to -1 as k approaches to -1. This
makes sense in contrast with our change of a; when a changes
the height of the graph changes. Changing k, we keep fix y
but then x changes. The height of the gaphs is always 1.
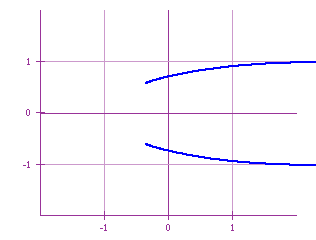
For k < -1 the behavior is similar, the line x = -1 acts as a
mirror, and for smaller values of k the graphs seems to be going
more to the left.
Now, what happens when k = -1? Observe that for this case, we get
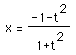 , so we obtain the value x = -1. This explains the 'inversion'
of the graphs for k=-1.
, so we obtain the value x = -1. This explains the 'inversion'
of the graphs for k=-1.