Chapter 1: Examining Distributions

Section 1.1: Displaying Distributions with Graphs

Categorical variables: Bar graphs and pie charts

For several good description of statistics, see the resources page: miscellaneous topics

Classification of Data

• Individual: An object described by a set of data.
• Variable: A characteristic of an individual.
     examples: height, weight, social security number, grades.
• Categorical Variable: places an individual into one of several groups or categories.
     examples: social security number, course grades.
• Quantitative Variable: takes numerical values.
     examples: height, weight, test grades.
• Distribution of a variable: describes what values the variable takes and how often it takes these values.

Exploratory Data Analysis (EDA) uses graphs and numerical summaries to describe the variables in a data set and the relations among them.

Strategies for EDA:

1. Examine each variable individually, then examine relationships among them.
2. Graph the data.
   • TYPES:
     • Pie charts
     • Bar Graphs
     • Histograms
     • Stemplots
     • Time plots
3. Numerical summaries of specific aspects of the data.

Chapter 1 considers single variable statistics

Graphs for categorical (a.k.a. qualitative) variables:

1. Pie charts:
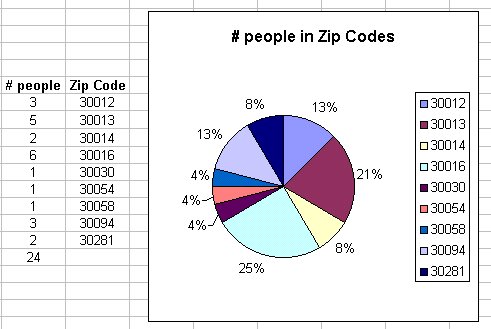
Here is the class separated into groups by zip code and graphed with a pie chart

Note that the area of each slice is proportional to the percentage of people in each zip code.

This chart was made with MS Excel.

2. Bar graphs:
Using the same data as above:

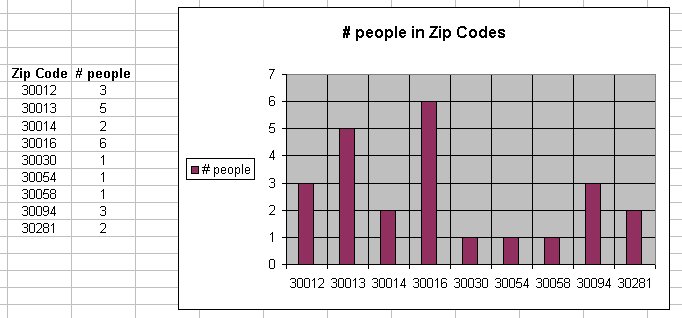
Note that the heigth (or area) of each bar represents the number of people in each zip code.

This chart was made with MS Excel.

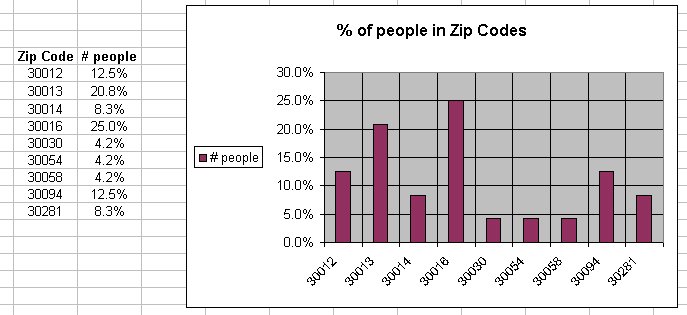
Note that the heigth (or area) of each bar represents the percentage of people in each zip code. Percentages are preferred for large data sets.

This chart was made with MS Excel.

These are limited in analyzing data since we can typically 'see' the same relationship among the numbers from the numbers themselves. In addition, for the pie chart we need to include all the categories that make up a whole and for the bar graph using percentages, you need the total number of observations. Often, we do not have access to the total.

Quantitative variables: Histograms

Steps in constructing a histogram:

1. Divide the range of values of the variable into classes of equal width
   (max - min)/(# of classes)
2. Count the number of observations in each class
3. Make a histogram

Choose classes wisely. The class width affects the graph of the data. To see this effect, here is a java demonstration of how class width affects a histogram.

Percentages are preferred for large data sets.

Here are the steps in constructing a histogram using a TI-83 calculator.

NOTE: In order to be able to use the TI-83 calculator to construct a histogram, you need the actual observations and NOT the percentages of observations

Interpreting histograms

Here are the characteristics of a histogram to consider:

• Overall pattern and any deviations
• Shape, center and spread
  • Shape: is the shape symmetric?, are there major peaks?, . . .
  • Center: the midpoint of the data. In other words, the point where 1/2 of the data is to the left and 1/2 of the data is to the right
  • Spread: the min value to the max value
• Look for possible outliers

We will be more specific about center and spread in section 1.2.

Skewed distributions:

• Skewed to right: if the right side of the distribution extends further out than the left side.
  In other words, if the (max – center) > (center – min).
• Skewed to left: if the left side of the distribution extends further out than the right side.
  In other words, if the (max – center) < (center – min).

The first step in determining if the distribution is skewed is to find the center, the max and the min. The center is found by counting through the number of observations until the half-way point is reached. However, suppose you are given the following histogram:

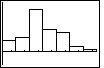
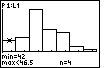
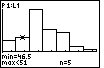
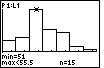
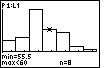
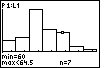
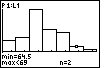
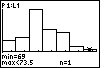
The above distribution looks skewed. To quantitatively determine the skeweness, count how many observations are in the above distribution by looking at the height of each bar. There are 43 observations. Thus, the center is at position 22. The 22^nd observation is in the third bar of the histogram. The far-right observation (in the far-right bar) is further from the center than the far-left observation (in the far-left bar). Thus, the distribution is right-skewed.

Quantitative variables: Stemplots

Stemplots work best for small numbers of observations.

The Leaf is the final digit in each observation. The Stem is all the other digits

Steps in constructing a stemplot:

1. Separate each observation into stem and leafs.
2. Write the stems in a vertical column with smallest value at top. Do not skip numbers in the stem.
3. Write each leaf in a row to the right of the stem in increasing order.

If there are too many digits, you may round the data.

You can split the stems (i.e., each stem appears twice). The upper stem will have leafs 0-4 and the lower stem will have leafs 5-9. For an example, see the top of page 17 of your text.

Back-to-back stemplots are useful when we wish to compare two related distributions.

Here are the steps in constructing a stemplot using a TI-83 calculator.

Time plots

Time plots are used when data is measured over time. They can reveal trends, or other changes over time.

Here are the steps in constructing a time plot using a TI-83 calculator.

Exploratory Data Analysis (EDA)

Preliminary examination of data sets:

• What kind of individuals?
• How many variables are present?
• What is the exact definition of the variable? What type? In what units? How is the variable measured?

Examination of graphs:

• Is shape symmetric or skewed?
• What is the center?
• What is the spread?
• What are the possible outliers?
• Is there a trend? (time plots only).