
To observe a GSP sketch that illustrates the effect of both the shape
of triangle ABC and the position of the point p click
here.
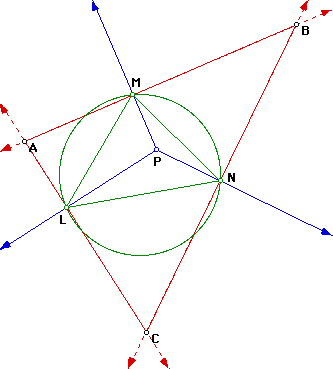
If we allow the point P to lie on the circumference of a circle then the
feet of the perpendicular will be collinear and the line formed is called
the Simson line. To view the Simson line click
here.
The point (P) is a specific example of a series of points known as the Miquel
point.