Task B
Take any triangle ABC. Construct squares externally on each side and locate
the center of each square. Label these centers A', B' and C' for the squares
opposite angles A, B and C.
Construct lines AA', BB' and CC'. Observe. Are they concurrent? Is the point
of concurrency any of the orthocenter, centroid, incenter or circumcenter
of triangle ABC? If not what can you find out about this point.
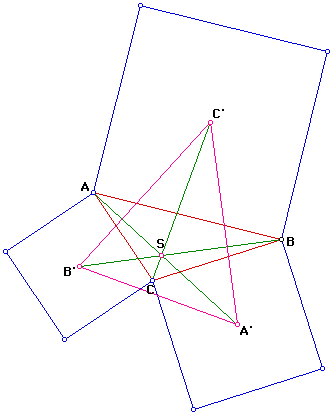
The point S (the cuncurrency of lines AA', BB' and CC') is discussed
fully in Task D though the fact that the lines
are concurrent is not proved!
Back

