

Introduction
Heron's formula is a geometric idea and Heron's development of it would have used geometric arguments. One such geometric approach is outlined here. It is the approach usually found in references.
Consider the figure at the right.
ABC is a triangle with sides of length BC = a, AC = b, and AB = c. The semiperimeter is
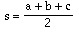
The circle with center O is the inscribed circle (incircle) of the triangle with points of tangency at D, E, and F. Triangles AOB, BOC, COA all have an altitude equal to the radius of the incircle (r = OD = OE = OF) so
Point H is constructed on the extension of BC such that BH = AF. Therefore CH = s. The area of the triangle is Area = (OD)(CH) = rs.
A perpendicular to CB is constructed at B and a perpendicular to OC is constructed at O. L is the intersection of these two perpendiculars and K is the point of intersection of OL with CB.
Click here for a GSP sketch of the figure which you can manipulate.
The proof can be constructed by considering similar figures (e.g., triangles AOF and CLB), the area as the sum of the areas of the triangles BOC, AOC, and AOB, and appropriate substitutions.
For similar approach to a geometric proof, see Umbarger (2000). This is a completed proof so don't go here until you have tried to construct your own proof.