
Lesson #1: Angles
By Rebecca Adcock
Two
fundamental concepts in trigonometry are angle and angle measure. An angle is
formed by rotating a ray around its endpoint. The endpoint of the ray becomes
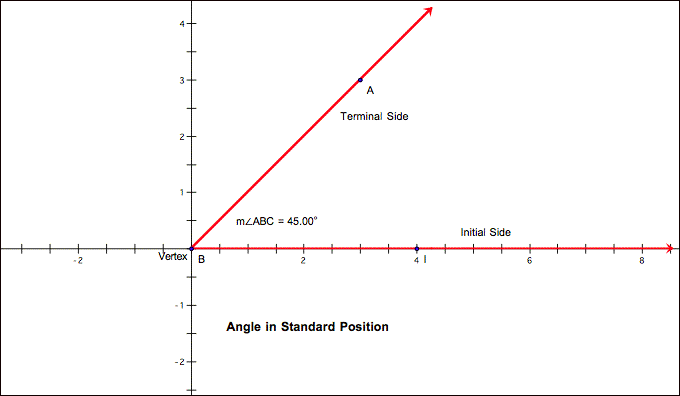
the vertex of the angle. The starting position of the ray is called the initial
side of the angle. The ending
position is called the terminal side. An angle in standard position has its initial side on the positive x-axis so the
vertex is at the origin.
Angles in Standard and
Non-standard Position
Positive and Negative
Angles
The
measure of an angle describes the magnitude and direction of the rotation of
the ray from its initial position to its terminal position. If the rotation is
counterclockwise, the angle has a positive measure. If the rotation is clockwise, the angle has a negative
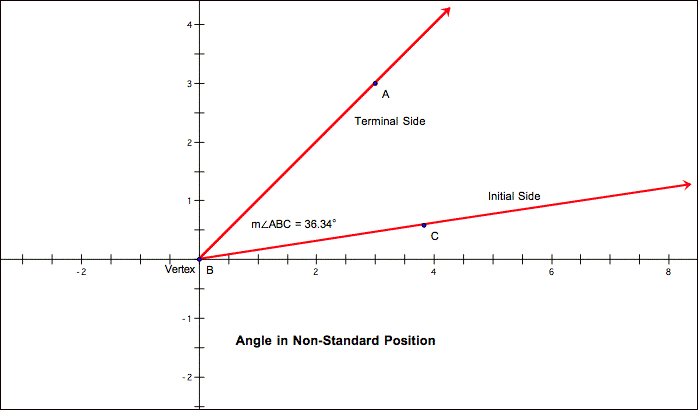
measure. An angle in standard
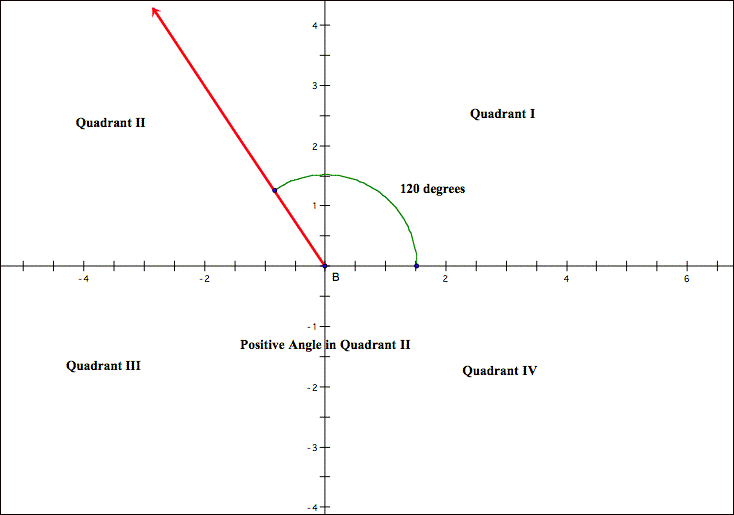
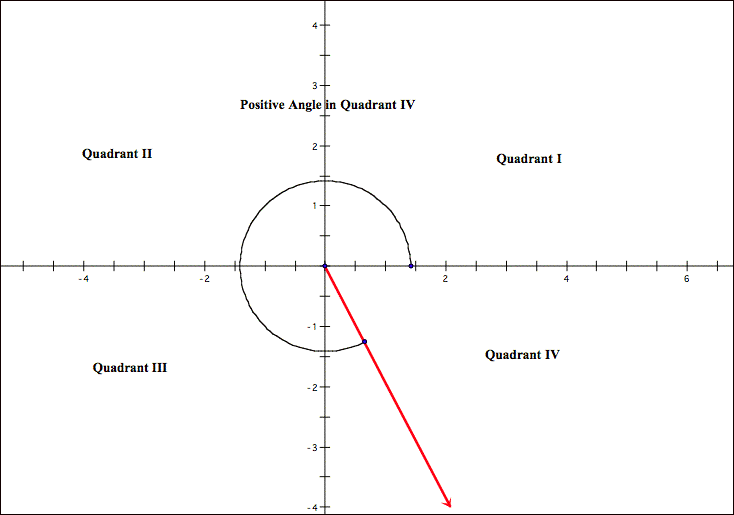
position is said to lie in the quadrant where the terminal side resides.
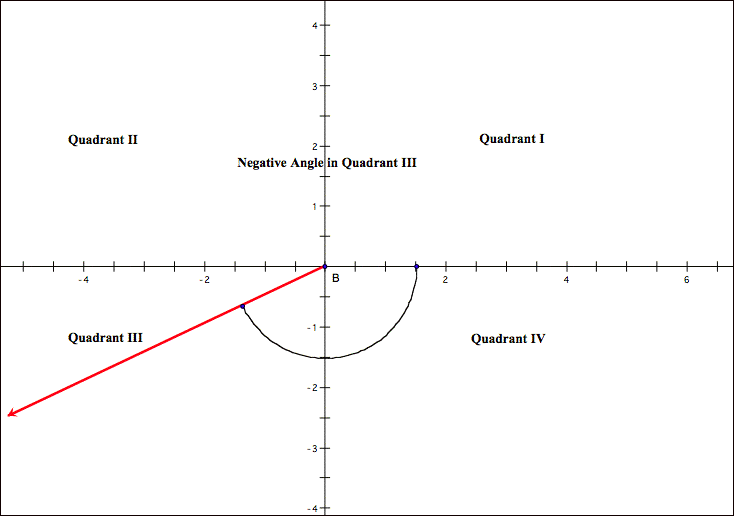
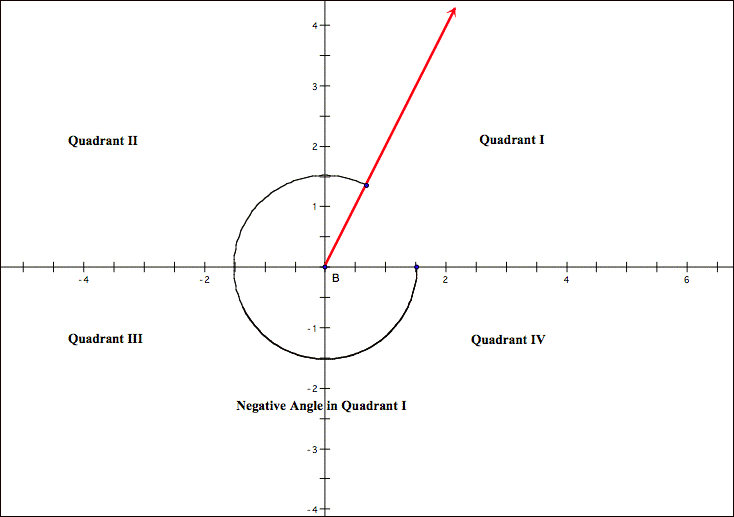
Coterminal Angles
One
way to measure an angle is in degrees. An angle created by one complete counterclockwise
revolution measures 360°. One
generated by one complete clockwise rotation is -360°. An angle may have a degree measure that
is multiple of 360° or a fractional part of it.
Two or more angles in
standard position can share the same terminal side and have different degree
measures. These angles are called coterminal.
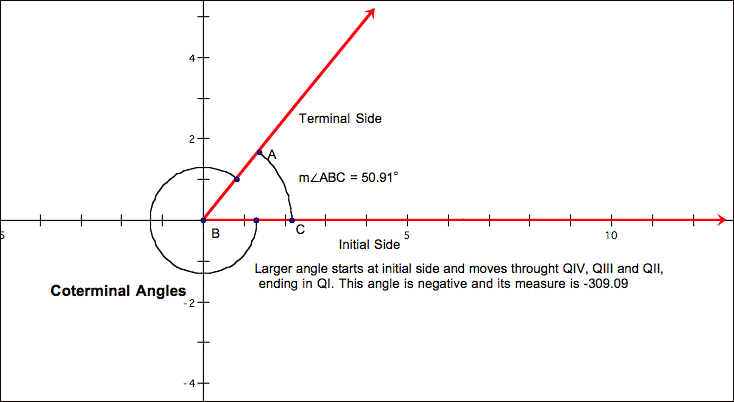
If θ is the degree
measure of an angle, then all angles coterminal with this angle have a degree
measure of θ+360k where k is
an integer. Using this formula for the example above where θ is 50.91°, -309.09° = 50.91°+(-1)360°. (Value of k is -1 and the angle was created on the
first revolution of a ray in a negative direction.)
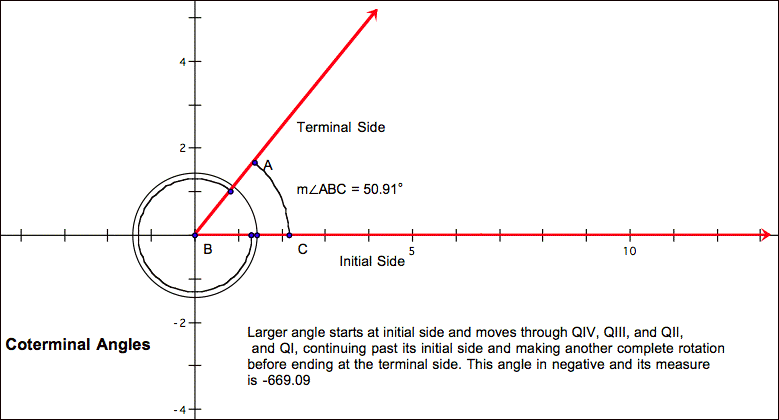
Again using the
formula “θ+360k where k is an
integer”, we can verify that an angle with measure -669.09° is coterminal to an angle with measure 50.91°. Where θ is 50.91°,
-669.09° = 50.91°+(-2)360°. (Value of k is -2 and the angle on the second
revolution of a ray in a negative direction.)
The point you need to
remember from all of this is that there are an infinite number of angles that are coterminal to any given angle. We
can go around in circles forever in either a negative or positive direction
creating coterminal angles. The measures of all the angles will differ by
multiples of 360 ° times some integer.
Reference Angles
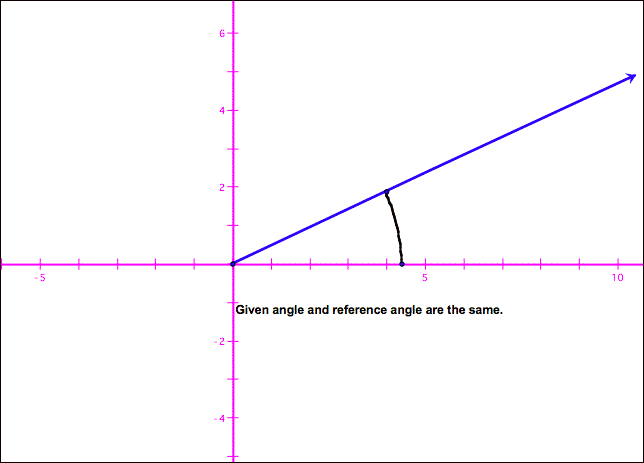
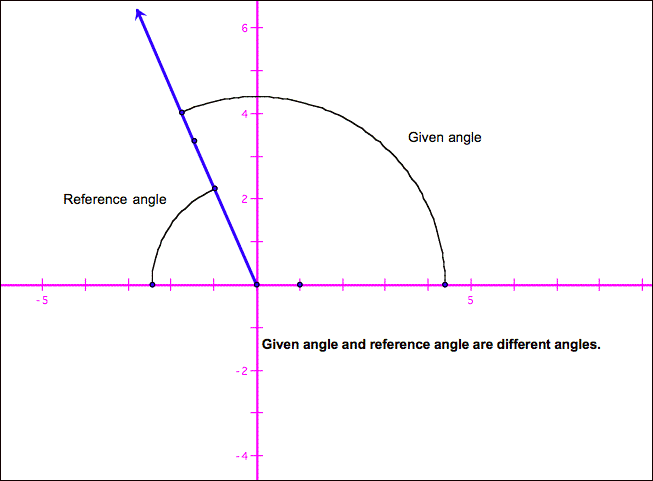
A useful tool for finding
values of trigonometric functions of certain angles (you’ll learn how to do
that later) is the reference angle. The reference angle is the acute angle
formed by the terminal side of a given angle and the x-axis. A reference angle
may be the same as the given angle.


Things to remember about
reference angles:
Š
A reference angle is
always ACUTE.
Š
A reference angle is
always measured to the x-axis.
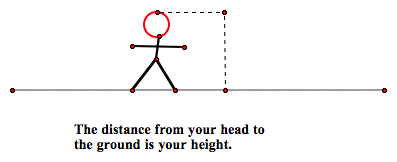
Remember it this way: measuring a reference angle to the x-axis is like
measuring your height from the top of your head to the ground. That makes
sense! Measuring a reference angle to the y-axis is like measuring your height
from the top of your head to a tree. That doesn’t make sense!

…..Don’t measure a
reference angle to the y-axis……………...measure it to the x-axis….
Check your understanding. See Lesson #1 in Lesson
Assessments.
Return to Main
Menu