Lesson #2: Radians

By Rebecca Adcock

Angle Measures in Radians

Angles have traditionally been measured in degrees. At some point the degree measure of a circle was determined to be 360°. (I don’t know who made that decision but it seems to work out ok!) Another unit for measuring angles is the radian and it is related to the radius of a circle.

It’s time for an activity, so STOP READING and go find three round objects to measure and some string. You will need to measure the radius so a basketball won’t work. If you’re at home, go into the kitchen and find a skillet, a dinner plate, and a drinking glass. Or something similar.

For each object, cut a string to the length of the radius and use the string to measure the circumference. Of course the string is a lot shorter than the circumference so you will have to keep track of how many times you have to move the string end-to-end to go around each object once. You’ll also have to mark your beginning point on each circumference so you know where to stop measuring.

Make a chart and enter your measurements.

Object

Circumference measured by lengths of string

Remember to cut a new length of string for each object. You don’t want to measure the circumference of the skillet with the radius of the drinking glass.

You should discover that all of your circumferences should have measured between 6 and 7 lengths of string. WHY? Do you remember the formula C=2πr? Circumference (of a circle) equals two times pi times the radius. Your string had a length of r (radius). The number of lengths of string it took to measure a circumference were an approximation of 2π or 6.28. Your string was cut the length of a radius and so it is also the arc length of a radian. A radius is a straight line segment and the arc length is curved because it is part of the circumference but they have the same length. Look at this…

In the picture above….

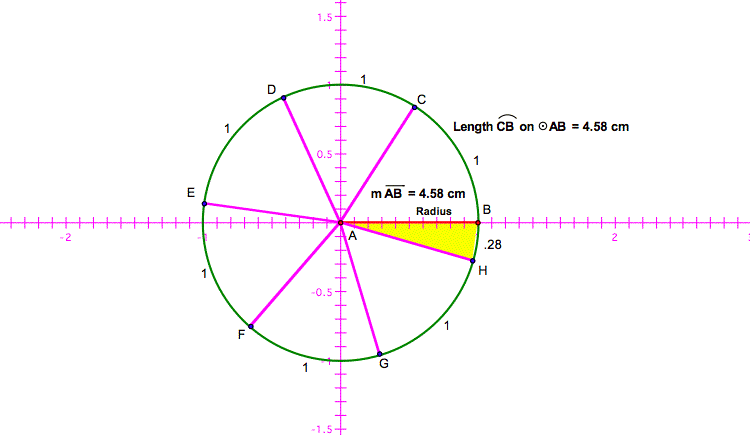
From point B to point C was one string length and therefore one radian. If measured as a straight line segment, the distance from point B to point C would be the same as the distance from point A (center of circle) to point B.

From point C to point D was one string length and another radian.

Repeat that for 5 more times, for a total of 6 radius lengths around the circle. The piece left over is approx .28. That’s the yellow slice. So the length of the radius wraps around the circumference approximately 6.28 times. Each ‘slice’ of the ‘pie’ above has an arc length of one radian except for the yellow slice.

We also know that one radian has a degree measure since it is an arc defined by a central angle. (A central angle is an angle whose vertex lies at the center of a circle.) To calculate the degree measure of a radian, divide 360° by 6.28. The result is 57.32°

You can see this in the picture below….

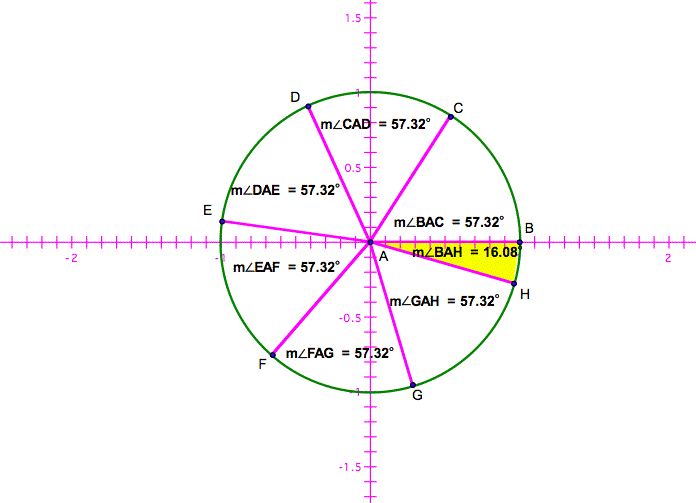
The little piece left over has a degree measure of 16.08 but we really don’t care about that because that arc did not represent a radian, it’s just what was left over.

So the most important thing to remember:

A central angle of a circle is an angle whose vertex lies at the center of the circle. When a central angle intercepts an arc that has the same measure as the radius of the circle, the measure of that angle is one radian.

Radians vs Degrees

Since it is possible to measure an angle in either degrees or radians, it may be necessary to convert from one unit of measure to the other.

To convert from degrees to radians:

Multiply the number of degrees by .

Example: Express 135° in radians.

Notice that the degrees in the numerator and in the denominator neutralize each other and disappear. This is an easy way to remember which formula to use. Just remember that you have to make the degrees disappear so you can use radians. Also note that π appears in the answer. When π is present, we assume the unit of measure is radians so we don’t have to state ‘ radians’.

To convert from radians to degrees:

Multiply the number of radians by .

Example: Express as degrees.

Notice that π in the numerator and denominator are 1 and disappear. Also note that the degrees are introduced in the numerator and remain in the answer as the unit of measure.

One last thing to do before you finish this lesson. Click on this icon to see an animated definition of a radian.

(“Radians Live!” is provided courtesy of Key Curriculum Press.)

Check your understanding. See Lesson #2 in Lesson Assessments.

Return to Main Menu.