Lesson #4: Trigonometric Functions

By Rebecca Adcock

Trigonometry is a branch of mathematics, related to geometry, that studies the relationships between the sides of triangles and their angles. Three of these relationships are the sine, cosine and tangent functions. In order to use and understand these functions, we first need to be able to determine a right triangle’s hypotenuse, and its opposite and adjacent sides.

Opposite and Adjacent Sides and the Hypotenuse

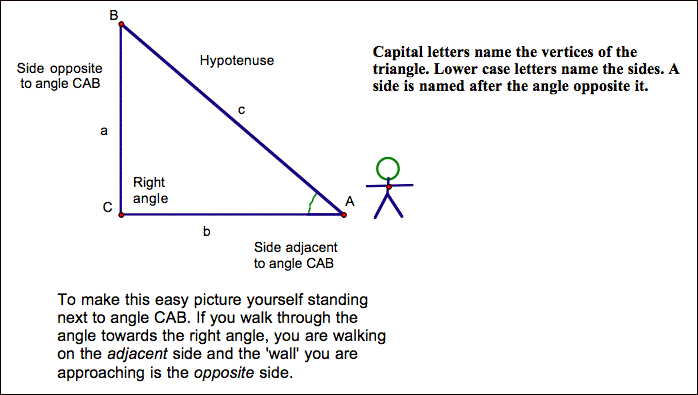
Opposite and adjacent sides are related to the angle under discussion. In the example at right, we are examining angle CAB.

Which side would be adjacent to that angle? We know side AB (also called c) is the hypotenuse because (1) it is the longest side and (2) it is opposite the right angle. So side AB is not the adjacent or opposite side. (Each side can have only one ‘job’ at a time.) The dictionary defines ‘adjacent’ as ‘nearby, adjoining, having a common endpoint or border.’ Side AC (also called b) fits the description. That means that side BC (also called a) would be the opposite side.

Ratios

A ratio is a comparison of two quantities in a particular order and it can be written as a fraction. In a right triangle, there are 6 trigonometric ratios.

The Big 3…… and Their Reciprocals Abbreviations

The Sine Ratio The Cosecant Ratio sine……...sin

Sine = length of the opposite side Cosecant = length of the hypotenuse

length of the hypotenuse length of the opposite side cosine…...cos

The Cosine Ratio The Secant Ratio tangent….. tan

Cosine = length of the adjacent side Secant = length of the hypotenuse

length of the hypotenuse length of the adjacent side cosecant….csc

The Tangent Ratio The Cotangent Ratio secant…….sec

Tangent = length of the opposite side Cotangent = length of the adjacent side

length of the adjacent side length of the opposite side cotangent…cot

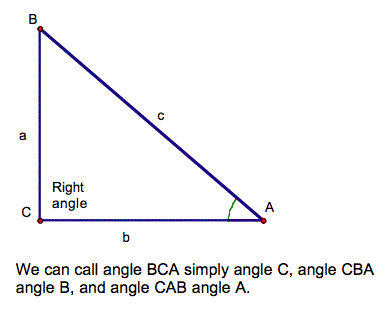
The Classic Example…

The Big 3… … and Their Reciprocals

sin A = opp = a csc A = hyp = c

hyp c opp a

sin B = opp = b csc B = hyp = c

hyp c opp b

cos A = adj = b sec A = hyp = c

hyp c adj b

cos B = adj = b sec B = hyp = c

hyp c adj a

tan A = opp = a cot A = adj = b

adj b opp a

tan B = opp = b cot B = adj = a

adj a opp b

How do we use all this information?

Suppose that you have a utility pole in your front yard and you want to know its height. A wire from the top of the pole forms a 30° angle with the ground and is anchored 25 feet from the base of the pole. How do you estimate the height of the pole?

Since the pole is vertical, it stands at a 90° angle to the ground and our problem can be represented as a right triangle.

The Legend of Sohcahtoa.

Remembering the formulae for the trigonometric functions has plagued mathematics students for eons. Somewhere in time, a creative (or desperate) individual decided to create a mnemonic to remember the formulae. That’s what Sohcahtoa is and here’s what it stands for….

S Sine =

O Opposite divided by

H Hypotenuse

C Cosine =

A Adjacent divided by

H Hypotenuse

T Tangent =

O Opposite divided by.

A Adjacent

There’s another story about Sohcahtoa… To read it, click here…. SOHCAHTOA http://www.pen.k12.va.us/Div/Winchester/jhhs/math/lessons/trig/legend.html

To return to this page, use the browser’s back key.

Check your understanding. See Lesson #4 in Lesson Assessments.

Return to Main Menu.