Lesson #5: Unit Circle

By Rebecca Adcock

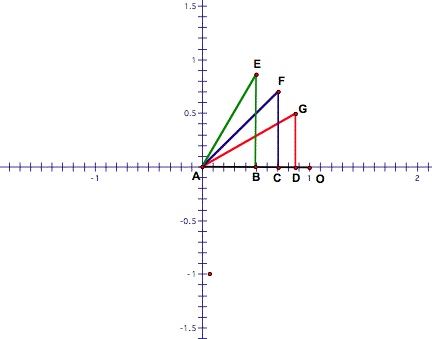
Recall the special triangles we studied in Lesson #3: Triangles. They looked like these.

The sides of these triangles are not drawn to scale but the angles measures are true. We will assume that the hypotenuse of each of these triangles has a measure of 1 unit. (We’re not specifying inches or centimeters or miles.) Now we’re placing these three triangles onto the Cartesian plane so that Point A of each lies at the origin and the side adjacent to A lies along the x-axis.

If we draw a circle with a radius of 1 unit and centered at A , the circle passes through points E,F, and G.

The definition of a unit circle is a circle with a radius of 1.

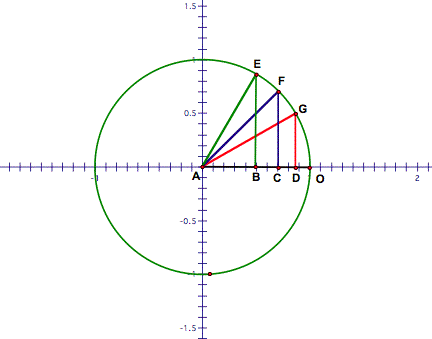
We can now use the lengths of the sides of our triangles to assign coordinate pairs to points E,F, and G. We can use the length of side AD of the red triangle ADG (which is ) to be the X-coordinate of G and the length of side DG (which is ) to be the y-coordinate of G . Similarly, we can define E and F.

We can also assign each of these points a value in terms of pi. Since the red line forms a 30 degree angle with the positive x-axis and the top half of the green circle is 180 degrees, then proportionately angle GAD is . Since it is of the half circle, it is also of p because half of a circle is equivalent to p. So Point G and angle GAD can be referred to as .

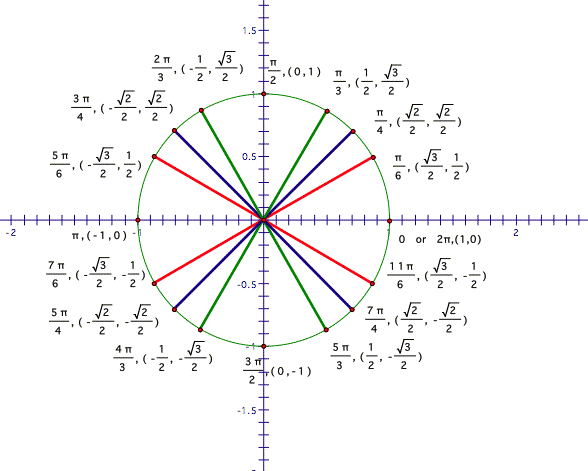
Expanding the first quadrant information to all four quadrants gives us the complete unit circle. We can assign each of the points on the circle an ordered pair and a value of pi just as we did above for the first quadrant. We can also sign coordinates to the points where the unit circle intersects the x-axis and the y-axis.

We define sin(x) as the y-coordinate of a point on the circle. So the y-coordinate for is . We define cos(x) as the x-coordinate of a point on the circle. So the x-coordinate for is .

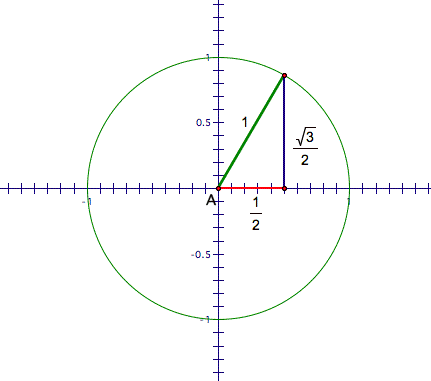
To see where this comes from, let’s apply our knowledge of sine and cosine to the picture above. We know that sine is the ratio of the length of the opposite leg to the length of the hypotenuse. So … or . We also know that the cosine is the ratio of the length of the adjacent leg to the length of the hypotenuse. So… or .

Because they are defined using the unit circle, it’s no wonder that the sine and cosine functions are often called circular functions. One final word…. Look back at the fully labeled unit circle and notice that the values of x and y of the ordered pairs range between -1 and 1. So we can state….

You’ll see that again in Lesson #6.

Check your understanding. See lesson #6 in Lesson Assessments.

Return to Main Menu.