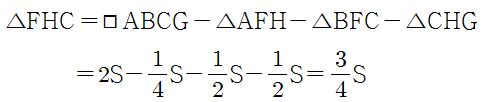Triangle of medians
by Hwa Young Lee
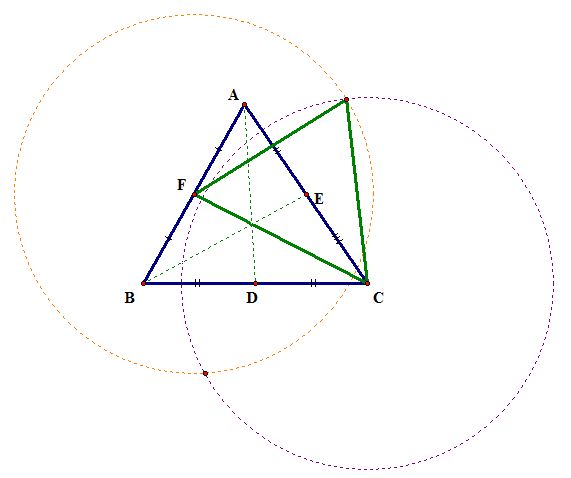
In assignment 4, we investigated a few properties of the centroid. The centroid is the intersection of the three medians of a given triangle.
Here we are going to construct a second triangle with the three sides having the lengths of the three medians from the original triangle.
Here's one way we can construct the triangle of the medians of the original triangle ABC:
Try to figure out how the triangle was constructed. Can you find any relationships between the two triangles?
First, we conjecture that the area of the triangle of medians is
the area of the original triangle.
To prove this, we are carefully going to construct our triangle of medians.
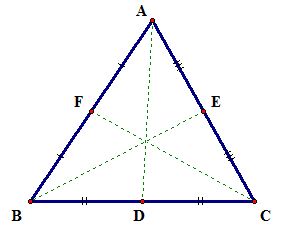
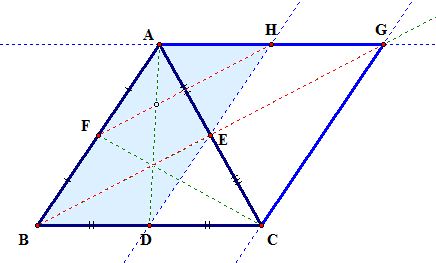
Step1) Construct our original triangle ABC and it's medians:
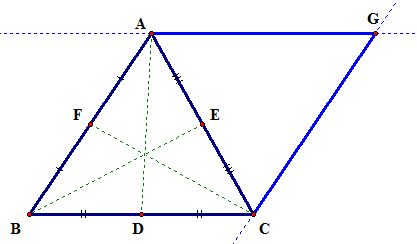
Step2) Construct a parallelogram ABCG that has side AB and BC like the following:
Step3) Construct a line that passes through the two midpoints D and E. Let's name the intersection of lines DE and AG as H.
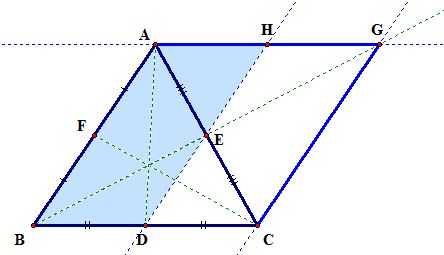
Then by the midpoint theorem, line DE is parallel to segment AB and thus we obtain parallelogram ABDH.
From this, we can easily prove that H is the midpoint of segment AG.
Step4) Connect midpoints F and H.
Then again, by the midpoint theorem,
.
Since the two diagonals of a parallelogram intersect at their midpoints, E is the midpoint of
and
.
Step5) Connect points H and C.
Then Since
, we obtain another parallelogram ADCH.
Hence,
.
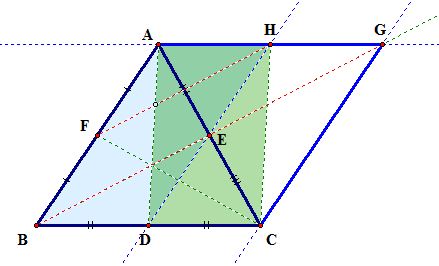
Step6) Connect our two midpoints F and C and we're done!
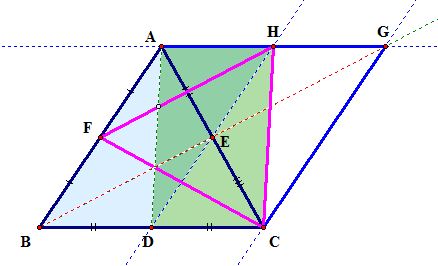
We have constructed triangle FHC of the medians of triangle ABC!
Now, since we carefully constructed our triangle FHC (we did not draw it by measuring the lengths of the medians nor did we drag them to form the triangle), we can use this construction to show that
.
Let us say the area of triangle ABC is S. Then
.
Also, since
,
.
Then the area of
And our proof is done.
Click here for a GSP sketch to manipulate. Try moving point A around to explore various kinds of triangles.
If the original triangle is equilateral, since the medians are all of the same length, the triangle of medians is equilateral as well.
If the original triangle is isosceles, the two medians formed by connecting the midpoints of the two equal length sides with their opposite vertices are of the same length. Thus, the triangle of medians is isosceles as well.