The cycloid
by Hwa Young Lee
In assignment 10, an example was left unanswered. Here, we will explore the example.
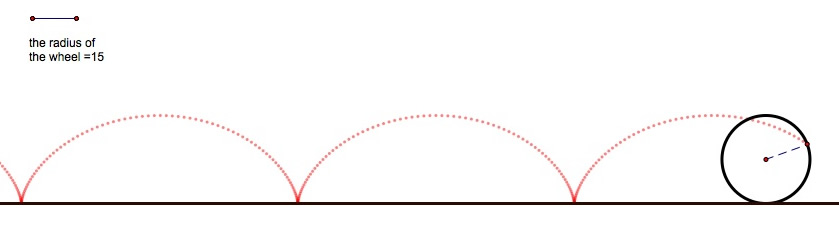
Example) Matt discovered a lump of gum stuck to the front tire of his bicycle. He became curious of the movement of the gum as the bike was gliding along the road. Assuming the road is flat, the bike is gliding along a straight line, and the tire is a perfect circle with radius 15 inches, what would the locus of the gum (a fixed point on the circle) be?
Here is a GSP animation of this situation
The locus of a fixed point on a circle rolling along a line is called a cycloid. Finding parametric equations for the cycloid in Matt's case.
In this situation, the circle is rotating so the gum (a fixed point) on the circle is moving along the circle as the circle rotates.
So, like the fly example in assignment 10, the parameter for this case would be the angle of the rotation.
Now, let's position the circle and fixed point on the xy-coordinate plane and find the parametric equations.
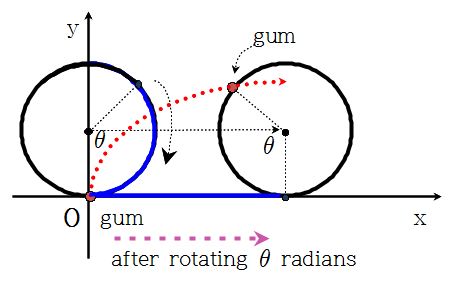
In Matt's case, there isn't a specific starting point, so let's say the gum starts at the origin.
Now, let's give some names for convenience.
First, let's name our gum as point P.
Second, let's say that the circle with radius of r rotated
radians.
Third, let the point on the circle that forms the arc of
named A.
Our goal is to find the equations in terms of
for the x-coordinate and y-coordinate of point P.
Then after
radians, point A would be on the x-axis. How do we find x and y?
Well, point P is decided by the angle of rotation and the position of the circle at that angle.
We know our angle of rotation is
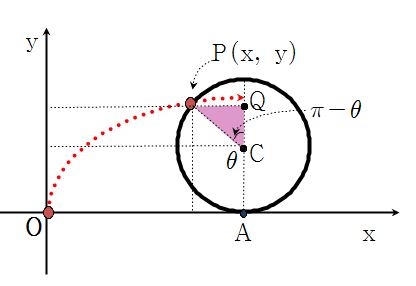
, so now we find the center of the circle (which tells us the position of the circle), say, point C.
The x-coordinate of point C would be equal to
.
Notice that this is the arc of the circle with central angle
(these same values are colored in blue).
Thus,
.
The y-coordinate of the center would be equal to the radius, so we obtain the center of the circle.
Now with these results, we find the coordinates of our gum (point P).
Before we start, let's name the intersection of the diameter perpendicular to the ground (x-axis) and horizontal line that passes through point P as Q.
Let's start with x.It is easy to see that
.
To find
, we use trigonometry.
If we take a look at the pink right triangle,
.
Hence,
For y,Again, taking a look at the pink right triangle and using trigonometry, we have
.
Hence,
.
Therefore, the parametric equations for the locus of the gum are
!
In Matt's case, the radius of the circle was of 15 units, so we have
Try changing the radius of the circle (wheel) in the animation and see what the cycloid looks like.