

A parametric curve in the plane is a pair of functions
where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t. In this investigation I allowed t to vary from 0 to 2pi. In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location. (This description is so well spoken because it was copied from the emat 6680 class page where assignment ten is presented. To link to assignment ten, click here, to access the 6680 class page, click here.)
Since the concept of a parametric curve is not the simplest type of mathematical concept, the discussion here will be limited to parametric equations of the form
To graph these curves using Graphing Calculator 3.0 the equation must look like
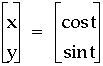
The visual representation of this form is seen below
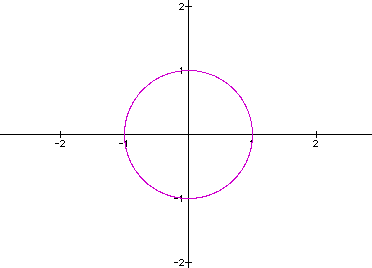
Note this is the familiar unit circle which is the basis of many trigonometric discussions. This follows logically because the x value of the points on the unit circle is determined by finding the cosine of the angle intersecting the circle. Of course, the vertex of the angle of which I speak is at the origin and the terminal side of the angle is along the positive x axis. To determine the y value of a point on the unit circle, the sine of the given angle is determined. This is just another example of how important the unit circle is to mathematics.
Next, I would like to see what happens to the parametric graph if t is multiplied by some constant. Below view a graph of this phenomena.
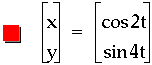
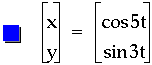
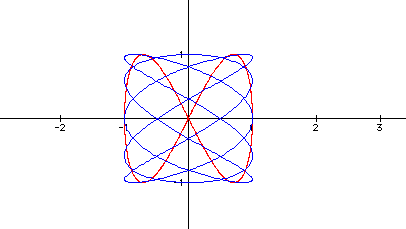
My first impression is simply, WOW. By investigating a bit further some conclusions may be reached. First notice that the graph has the same maximum and minimum x and y values as the unit circle. So one is lead to the question, "What affect did multiplying by the constants have?". Notice the red image meets the boundaries of the x-values at two points and the boundaries defined by the y-values at four points. Surely this relates directly to multiplying by two and four. One may say that the unit circle also meets its boundaries on the x-axis at two points, but the difference is that here the red curve also intersects the origin. We can see the blue graph meets the boundary created by the positive x value at five points and meets the bound created by the positive y value at 3 points. Why does it seem different when multiplying by an even or an odd? Clicking here, will allow the reader to check his hypothesis as this link goes directly to the file used to create the graph seen above.
One may be curious to see what happens if t is multiplied by a number less than one. See an example below. Click here to access the file that created the image below.
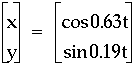
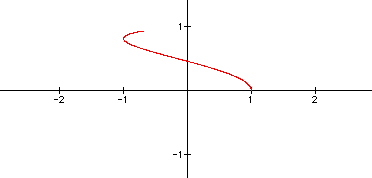
Here we note that multiplying by a number less than one, simply yields a piece of the graph that we saw when t was multiplied by a number greater than one. It may be deemed interesting to view a graph where both t's are multiplied by a number less than one. See below to view a graph of this occurrence.
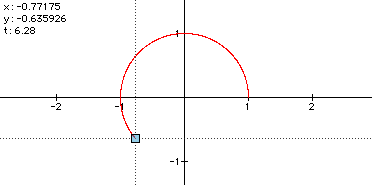
Using our knowledge of the unit circle, we can determine the angle which gives the shown x and y values. Dividing this angle measure by 360 shows that this is 61 percent of the unit circle. What do you suppose the t's were multiplied by? Click here to check your assumption.
In my opinion, it is more interesting to view graphs where t is multiplied by larger numbers. See an example below
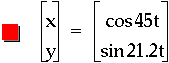
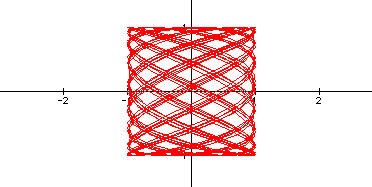
Again note that the entire graph is contained between -1 and 1 on both the x and y axes. This picture becomes even more interesting when the constants chosen to multiply by t are multiples of one another. See some examples below.
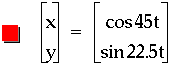
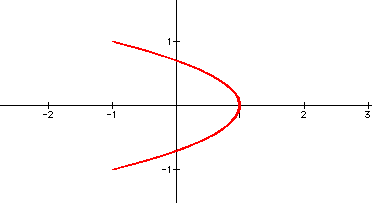
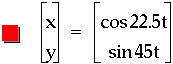
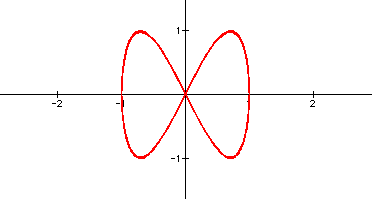
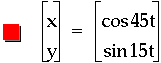
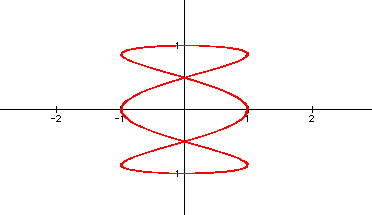

An explanation of why multiplying the t's by multiples does not give the complex graphs one may expect, but instead rather simple curves is that the relation maps to this particular values more than once. Notice the thick line representations. To experiment with this more, click here and adjust the values multiplied by t as you see fit.
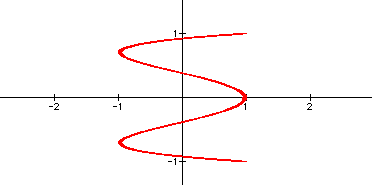
Well by now the reader, as well as myself, is probably curious to see if these graphs can break past the boundaries of the unit circle, namely -1 and 1 for the two axes. In order to see if this desire can be fulfilled let's multiply the cosine and sine by constants. Examples of what occurs can be seen below.
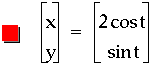
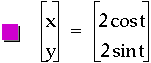
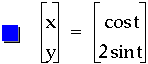
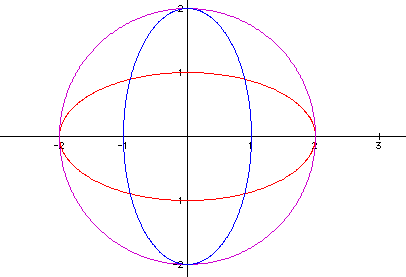
Notice the red curve reaches to -2 and 2 on the x-axis and the cos (t) was multiplied by two. The purple curve's boundaries are at -2 and 2 on both axes and each trigonometric function is this equation was multiplied by two. By viewing the blue curve, whose boundaries are -2 and 2 on the y-axis and noting that the sin (t) was multiplied by two, hopefully it is clear what must be done to cause the graph to break out of the unit circles boundaries. It seems clear to me that if one wishes for the curve to stretch or shrink to a particular bound all that needs to occur is multiplication of the trigonometric function by that particular value. See below to verify my statement as correct. If the reader wishes to experiment with values of his own, click here for access to a file that will allow for experimentation.
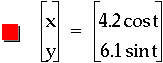
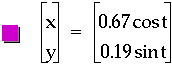
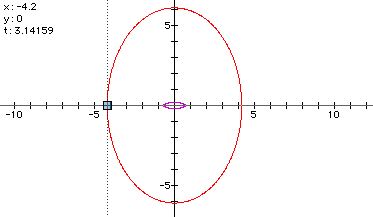
Naturally the next step is to consider equations where both t and the trigonometric functions are multiplied by constants. From what has been presented earlier in this investigation, it seems that the number multiplied by the trigonometric function will define the bounds of the graph and the values times t will create the number of points that reach these boundaries. Below is a visual representation of this thought and clicking here will access the file that created the image so the reader may create his own graphs.
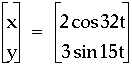
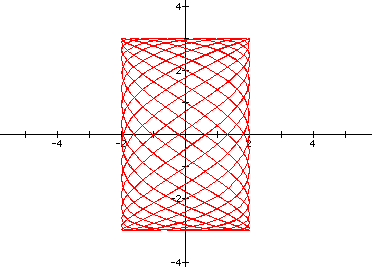
See another interesting example below.
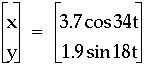
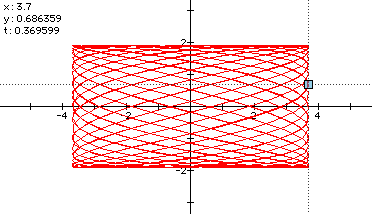
In conclusion, the graphs of this type of parametric equation relate directly to the unit circle. Multiplying both the trigonometric functions and the t's by constants creates some very intriguing images.