

This investigation involves any triangle ABC, an interior point P and the lines from each vertex thru P to the opposite sides. Thus three new points are created, one on each side of triangle ABC. See one example below.
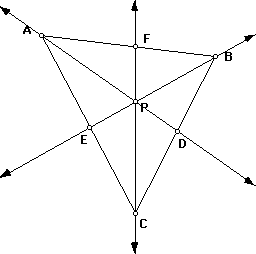
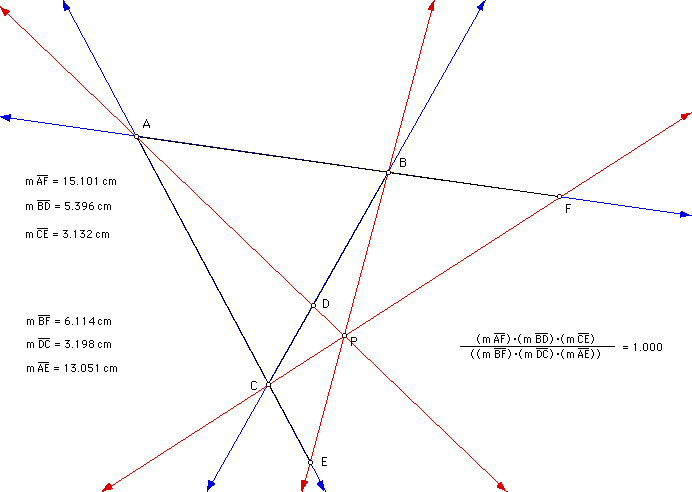
The problem posed based on this construction is to explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles ABC and different locations of the point P. With this in mind I decided to take advantage of the power of The Geometer's Sketchpad (GSP). Below is the construction I created with the various lengths of the segments in question as well as these particular products. To link to the GSP file used to create this sketch, click here. Once accessed, move P anywhere inside the triangle and note that for any position of P the products in question are always equivalent.
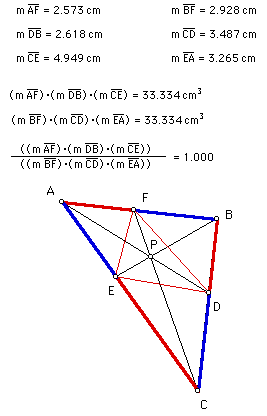
Since the ratio of the two products was one for every position of P I could find, I contend that it must be the case that the products are always equal. Let's prove this conjecture to be true.
With the idea that I am attempting to prove something about the ratios of sides of a triangle, I determine that it is necessary to find pairs of similar triangles involving the segments in the products. Because the benevolent Dr. Wilson suggests drawing pairs of parallel lines, I begin by looking for which lines I may construct that will be most advantageous. As it turns out there are three pairs that would be useful. These lines should be parallel to one of the lines through P and they must pass through the other two vertices. I choose to draw lines through A and B parallel to FC. Below is the sketch I considered for this proof.

First consider triangle APF and triangle AKB. By AA the two are similar. Angle FAP = angle BAK because they are really the same angle. Also, angle AFP = angle ABK since they are corresponding angles with relation to the parallel lines BK and FC. Knowing the two are similar allows me to write
Now realize that triangle BPF is similar to triangle BJA by AA. Again they each contain one angle, namely B, and they have pairs of corresponding angles which are congruent to one another since FC is parallel to AJ. Thus I write the proportion
By cross multiplying the proportions above we arrive at the two equations (AF)(BK) = (AB)(FP) and (BF)(AJ) = (AB)(FP). Therefore I can substitute to write (AF)(BK) = (BF)(AJ). From this equation the proportion
is determined.
Here we must consider some other pairs of similar triangles in order to arrive at our goal. Let's use a visual for assistance.
The shaded triangles AEJ and CEP are similar by AA. This fact is true since angle AEJ and angle CEP are vertical, and therefore congruent, and angles PCE and JAE are alternate interior angles with respect to the parallels CP and AJ, so they also must be congruent. This similarity yields the following proportion:
Now consider the following image.
Here the shaded triangles BDK and CDP are also similar by AA. Angles BDK and CDP are congruent because they are vertical. Also angles PCD and KBD are congruent since they are alternate interior angles with respect to the parallels BK and CP. Thus I may write the following proportion:
Now we have three proportions.
If we multiply the ratios on the left of each proportion we arrive a product which is the same as the product of the ratios on the right of each proportion, shown below.
Notice each term in the numerator of the right ratio is also in the denominator. Therefore the value of the right side of the above equation is one. Thus the left must be one as well, which allows us to write
hereby concluding the proof of my conjecture.
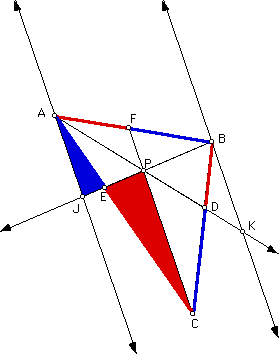
Next, I was asked to consider if this result could be generalized if triangle ABC were to be composed of lines and P were on the outside of the triangle. My answer is yes and I present the following GSP sketch in support of my claim. Click here to link to the file in GSP used to create the image below. Once there move P anywhere and see that this particular ratio is always one.
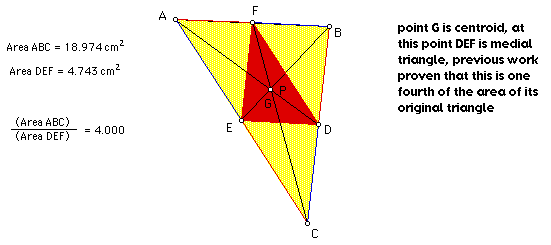
P at the centroid
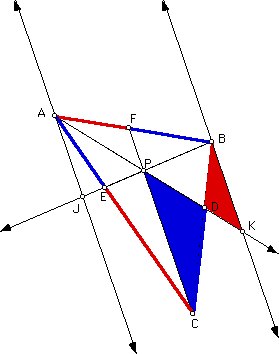
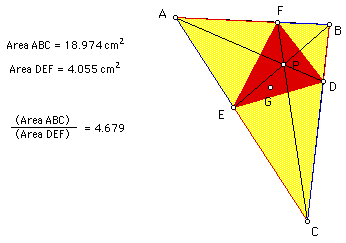
Another location of P
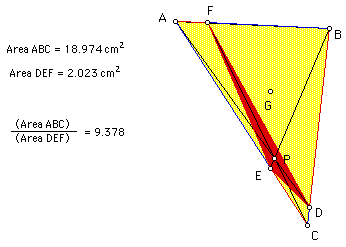
P at a third location
In conclusion, I find geometry more and more incredible each day. Just this one construction yields so many interesting theories. Certainly there will always be more things to learn in this discipline.