Write Up 8

by

Alison Hays

Problem: The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L, M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?

(This is problem 13 of Assignment 8.)

Given a triangle ABC, we need to construct the circumcircle, and we need to construct the internal angle bisectors of triangle ABC and extend them to meet the circumcircle at points L, M, and N, respectively.

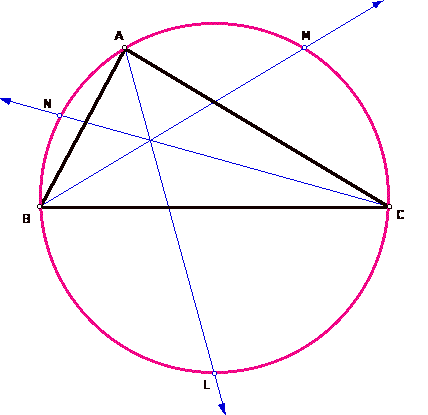
Now we need to construct the triangle LMN, and find a relationship between the measures of angles L, M, and N and the measures of angles A, B, and C.

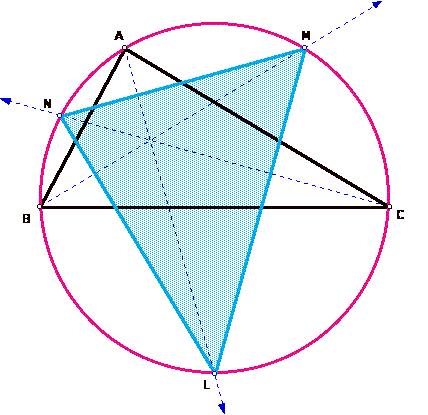
Click here to explore the angle measures using GSP.

After exploring the angles measures, we find the following relationships:

The measure of angle L is half the sum of the measures of angles B and C.
The measure of angle M is half the sum of the measures of angles A and C.
The measure of angle N is half the sum of the measures of angles A and B.

Click here to verify this relationship using GSP.

Now it's time to prove this relationship! Click here for the proof.