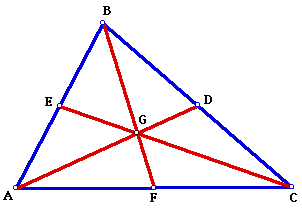
A median of a triangle is a line segment whose endpoints are the vertex of an angle of the triangle and the midpoint of the side opposite that angle. Every triangle has three medians that are concurrent (intersect in the same point). The centroid of a triangle is the point at which the three medians of that triangle intersect. In the figure below, line segments AD, CE and BF are the medians of triangle ABC. Point G is the centroid of triangle ABC.

Theorems related to medians and centroids:
1. Each median of a triangle separates that triangle into two triangles of equal area. For example, in the figure above, median BF separates triangle ABC into triangles ABF and triangle FBC. Triangles ABF and FBC have the same area. (Click here to see a proof of this theorem.)
2. The medians of a triangle separate that triangle into 6 smaller triangles of equal area. In triangle ABC above, the medians separate ABC into the 6 smaller triangles BGE, AGE, FGA, CGF, DGC and DGB. Each of these 6 smaller triangles has the same area. (Click here to see a proof of this theorem.)
3. The centroid of a triangle separates each median of that triangle into two smaller line segments whose lengths are in the ratio of 2:1 The centroid G above separates median BF into line segments BG and GF. BG is twice the length of line segment GF. (Click here to see a proof of this theorem.)