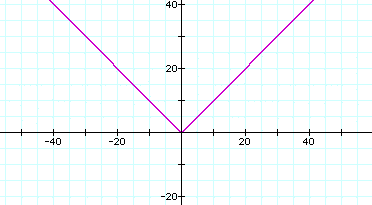
First, let us look at the parent function f(x) = |x|. The graph of this function looks like the following.
Notice that it is symmetric about the y-axis and looks like a v. Now, that we have the parent function and its graph. Let's look at thow the four transformations happen.
First, we must have a definition of the two types of translations. A vertical translation moves the graph up or down. An example of that would be:
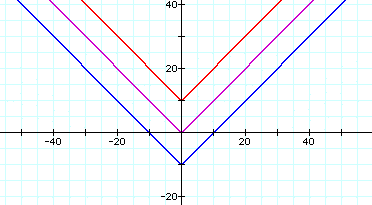
Here, the red graph has been moved up 10 units and the blue graph has been moved down 10 units. These are the two types of vertical translations.
The other type of translation is a horizontal translation. A horizontal translation moves the graph left or right. An example of this would be:
Here, the red graph has been moved to the left 10 units and the blue graph has been moved to the right 10 units.
Now that we have seen some examples of the these, let's see if we can figure out why these translations happen.
Here is an equation of one of the vertical translations: 
, which of the graphs
do you think it is? If you said the red one, you are correct.
Now, what do you think the equation of the blue graph is? If
you said, 
, then
you are correct again.
What does this lead us to any generalizations about how to make vertical translations with regard to our parent function? If you need a little more help, click here to start a movie of the parent function moving through vertical translations.
Now, we have hopefully come up with a generalization for our parent funcion, f(x) = |x|.
The Rule for Vertical Translations:
if y = f(x), then y = f(x) + k gives a vertical translation. The translation k moves the graph upward when k is a postive value and downward when k is negative value.
Here is an equation of one of the horizontal translations:
, which of the graphs
do you think it is? If you said the red one, you are correct.
Now, what do you think the equation of the blue graph is? If
you said, 
, then
you are correct again.
What does this lead us to any generalizations about how to make vertical translations with regard to our parent function? If you need a little more help, click here to start a movie of the parent function moving through horizontal translations.
Now, we have hopefully come up with a generalization for our parent funcion, f(x) = |x|.
The Rule for Horizontal Translations:
if y = f(x), then y = f(x-h) gives a vertical translation. The translation h moves the graph to the left when h is a postive value and to the right when h is negative value.
Remember that these translations do not necessarily happen in isolation. It is quite possible to have both a vertical and horizontal translation at the same time.