Examples: 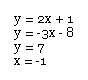
A polynomial is a monomial or sum or terms that are all monomials. Polynomials can be classified by degree, the highest exponent of any individual term in the polynomial. The degree tells us about the general shape of the graph.
As the degree increases above 1, the graph gets points of inflection where it changes direction. This change of direction causes a U-turn. These points of inflection give relative mins or maxes. Look at the chart below for some extra clarification.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Do you notice a pattern? You should, after the degree goes above 1, the number of turns in the graph is one less than the degree.
These are constants. In other words, numbers without variables.
Examples: 5, -100, .75, -3.6
If we graphed these, they would just be points on the number line.
These are lines with the general form: y = mx + b. They have no inflection points and some examples of these are:
Examples:
If you need a further review of lines click here to link back to topic 1.
These are parabolas with the general form:
They have one point of inflection and one U-turn. Examples of this type of equation would be:
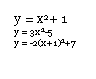
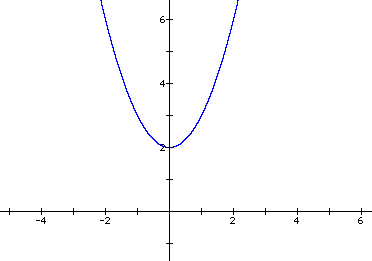
For further review of these see solving quadratic equations, topic 7.
These equations will have two U-turns and look like an S. They have two points of inflection and some examples of these would be:
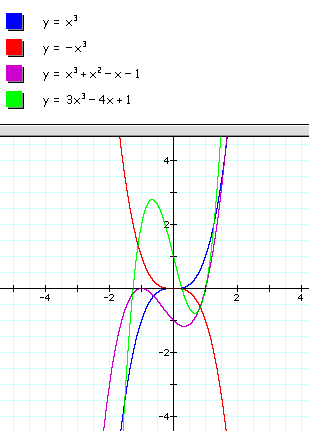
Notice how all of the different colored graphs have an S shape and in order to do that hav 2 U -turns.
These equations will have three U-turns and look like a W. They have three points of inflections and some examples of these would be:
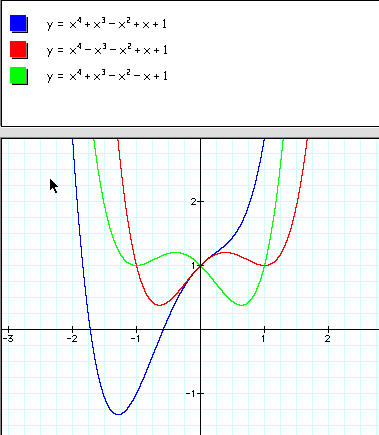
Notice how the different colored graphs have the shape of a W and 3 U-turns.
Now, you should have a good enough understanding of how to graph polynomials that you should be able to make predictions about the shape of the graph based on a given equation.